
【题目】如图,在四棱锥![]() 中,平面
中,平面![]() 平面
平面![]() ,底面
,底面![]() 是等腰梯形,
是等腰梯形,![]() ,
,![]() ,点E在线段
,点E在线段![]() 上,且
上,且![]() .
.
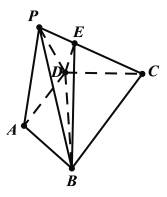
(1)证明:![]() 平面
平面![]() ;
;
(2)求二面角![]() 的余弦值.
的余弦值.
【答案】(1)证明见解析;(2)![]() .
.
【解析】
(1)连接![]() ,交
,交![]() 于点F,连接
于点F,连接![]() ,证得
,证得![]() ,由此可证明
,由此可证明![]() 平面
平面![]() ;
;
(2)取![]() 中点O,取
中点O,取![]() 中点H,连接
中点H,连接![]() ,
,![]() ,则
,则![]() ,以O为原点,以
,以O为原点,以![]() 方向为x轴,
方向为x轴,![]() 方向为y轴,以
方向为y轴,以![]() 方向为z轴,建立如图所示空间直角坐标系,利用向量法求二面角
方向为z轴,建立如图所示空间直角坐标系,利用向量法求二面角![]() 的余弦值.
的余弦值.
解:(1)连接![]() ,交
,交![]() 于点F,连接
于点F,连接![]() .
.
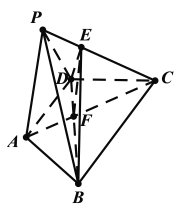
在等腰梯形![]() 中,
中,![]() ,
,![]() ,则
,则![]() ,
,![]() ,
,
又![]() ,则
,则![]() ,所以
,所以![]() ,
,
所以![]() ,
,
又![]() ,
,![]() ,所以
,所以![]() .
.
(2)取![]() 中点O,取
中点O,取![]() 中点H,连接
中点H,连接![]() ,
,![]() ,显然
,显然![]() .
.
又平面![]() ,平面
,平面![]() ,所以
,所以![]() .
.
由于O、H分别为![]() 、
、![]() 中点,四边形
中点,四边形![]() 是等腰梯形.
是等腰梯形.
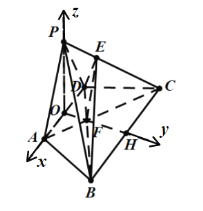
则![]() ,故以O为原点,以
,故以O为原点,以![]() 方向为x轴,
方向为x轴,![]() 方向为y轴,
方向为y轴,
以![]() 方向为z轴,建立如图所示空间直角坐标系.
方向为z轴,建立如图所示空间直角坐标系.
则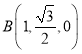 、
、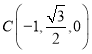 、
、![]() 、
、 ,
,
可得 、
、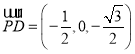 、
、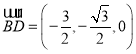 、
、
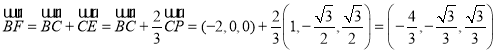 ,
,
设平面![]() 的一个法向量为
的一个法向量为![]() ,由
,由![]() 、
、![]() 可得
可得
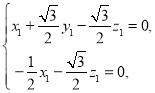
令![]() ,可得
,可得![]() ,
,![]() ,则
,则![]() .
.
设平面![]() 的一个法向量为
的一个法向量为![]() ,由
,由![]() 、
、![]() 可得
可得
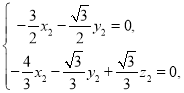
令![]() ,可得
,可得![]() ,
,![]() ,则
,则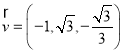 .
.
从而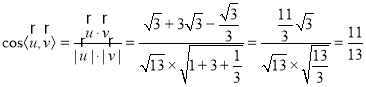 ,
,
则二面角![]() 的余弦值为
的余弦值为![]() .
.


 开心蛙状元作业系列答案
开心蛙状元作业系列答案 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案 一课一练一本通系列答案
一课一练一本通系列答案 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案科目:高中数学 来源: 题型:
【题目】“地摊经济”是李克强总理在本届政府工作报告中向全国人民发出的口号,某生产企业积极响应号召,大力研发新产品,为了对新研发的一批产品进行合理定价,将该产品按事先拟定的价格进行试销,得到一组销售数据![]() (
(![]() ,2,3,4,5,6),如表所示:
,2,3,4,5,6),如表所示:
试销单价x(元) | 4 | 5 | 6 | 7 | 8 | 9 |
产品销量y(件) | q | 84 | 83 | 80 | 75 | 68 |
已知![]() ,
,![]() ,
,![]()
(1)试求q,若变量x,y具有线性相关关系,求产品销量y(件)关于试销单价x(元)的线性回归方程![]() ;
;
(2)用![]() 表示用(1)中所求的线性回归方程得到的与
表示用(1)中所求的线性回归方程得到的与![]() 对应的产品销量的估计值.当销售数据
对应的产品销量的估计值.当销售数据![]() 对应的残差的绝对值
对应的残差的绝对值![]() 时,则将销售数据
时,则将销售数据![]() 称为一个“好数据”.现从6个销售数据中任取3个,求“好数据”个数
称为一个“好数据”.现从6个销售数据中任取3个,求“好数据”个数![]() 的分布列和数学期望
的分布列和数学期望![]() .
.
(参考公式:线性回归方程中![]() ,
,![]() 的最小二乘估计分别为
的最小二乘估计分别为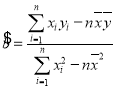 ,
,![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设f(x)=|lnx|,若函数g(x)=f(x)-ax在区间(0,4)上有三个零点,则实数a的取值范围是( )
A. (0,![]() )B. (
)B. (![]() ,e)C. (
,e)C. (![]() ,
,![]() )D. (0,
)D. (0,![]() )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com