【题目】在直角坐标系xOy中,曲线C的参数方程为 ![]() (α为参数)
(α为参数)
(1)求曲线C的普通方程;
(2)在以O为极点,x正半轴为极轴的极坐标系中,直线l方程为 ![]() ρsin(
ρsin( ![]() ﹣θ)+1=0,已知直线l与曲线C相交于A,B两点,求|AB|.
﹣θ)+1=0,已知直线l与曲线C相交于A,B两点,求|AB|.
参考答案:
【答案】
(1)解:曲线C的参数方程为 ![]() (α为参数),
(α为参数),
x,y平方相加可得:x2+y2=2,①
(2)解:直线l方程为 ![]() ρsin(
ρsin( ![]() ﹣θ)+1=0化为普通方程为:x﹣y+1=0,②
﹣θ)+1=0化为普通方程为:x﹣y+1=0,②
由②得:y=x+1,③
把③带入①得:2x2+2x﹣1=0,
∴  ,
,
∴|AB|= ![]() |x1﹣x2|
|x1﹣x2|
= ![]()
![]()
= ![]()
= ![]()
【解析】(1)把参数方程中的x,y平方相加即可得普通方程;(2)把直线l方程为 ![]() ρsin(
ρsin( ![]() ﹣θ)+1=0化为普通方程为:x﹣y+1=0,然后根据弦长公式计算即可.
﹣θ)+1=0化为普通方程为:x﹣y+1=0,然后根据弦长公式计算即可.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=ln(ax+
 )+
)+  .
.
(1)若a>0,且f(x)在(0,+∞)上单调递增,求实数a的取值范围;
(2)是否存在实数a,使得函数f(x)在(0,+∞)上的最小值为1?若存在,求出实数a的值;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知
 是双曲线
是双曲线  的右焦点,过点
的右焦点,过点  作
作 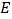 的一条渐近线的垂线,垂足为
的一条渐近线的垂线,垂足为 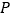 ,线段
,线段  与
与 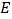 相交于点
相交于点  ,记点
,记点  到
到 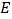 的两条渐近线的距离之积为
的两条渐近线的距离之积为 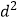 ,若
,若 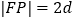 ,则该双曲线的离心率是( )
,则该双曲线的离心率是( )
A.
B.2
C. 3
D.4 -
科目: 来源: 题型:
查看答案和解析>>【题目】在一次趣味校园运动会的颁奖仪式上,高一、高二、高三代表队人数分别为120人、120人、n人.为了活跃气氛,大会组委会在颁奖过程中穿插抽奖活动,并用分层抽样的方法从三个代表队中共抽取20人在前排就座,其中高二代表队有6人.

(1)求n的值;
(2)把在前排就座的高二代表队6人分别记为a,b,c,d,e,f,现随机从中抽取2人上台抽奖.求a和b至少有一人上台抽奖的概率;
(3)抽奖活动的规则是:代表通过操作按键使电脑自动产生两个[0,1]之间的均匀随机数x,y,并按如图所示的程序框图执行.若电脑显示“中奖”,则该代表中奖;若电脑显示“谢谢”,则不中奖,求该代表中奖的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】国家射击队的某队员射击一次,命中7~10环的概率如表所示:
命中环数
10环
9环
8环
7环
概率
0.32
0.28
0.18
0.12
求该射击队员射击一次 求:
(1)射中9环或10环的概率;
(2)至少命中8环的概率;(3)命中不足8环的概率。
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=lnx,x1 , x2∈(0,
 ),且x1<x2 , 则下列结论中正确的是( )
),且x1<x2 , 则下列结论中正确的是( )
A.(x1﹣x2)[f(x1)﹣f(x2)]<0
B.f( )<f(
)<f(  )
)
C.x1f(x2)>x2f(x1)
D.x2f(x2)>x1f(x1) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,P是直线x=4上一动点,以P为圆心的圆Γ经定点B(1,0),直线l是圆Γ在点B处的切线,过A(﹣1,0)作圆Γ的两条切线分别与l交于E,F两点.
(1)求证:|EA|+|EB|为定值;
(2)设直线l交直线x=4于点Q,证明:|EB||FQ|=|BF|EQ|.

相关试题

