【题目】已知函数![]() 在点(1,f(1))处的切线为y=1.
在点(1,f(1))处的切线为y=1.
(1)求a,b的值;
(2)问是否存在实数m,使得当x∈(0,1]时,![]() 的最小值为0?若存在求出m的取值范围;若不存在,请说明理由.
的最小值为0?若存在求出m的取值范围;若不存在,请说明理由.
参考答案:
【答案】(1)a=1,b=2. (2)(-∞,2].
【解析】
试题分析:(1)求函数的导数,利用导数的几何意义,建立方程关系即可求实数a,b的值;(2)求函数的导数,利用函数的最小值,建立条件关系即可得到结论
试题解析:(1)因为![]() ,其定义域为(0,+∞),所以
,其定义域为(0,+∞),所以![]()
依题意可得![]() 解得a=1,b=2.
解得a=1,b=2.
(2)![]() ,
,
所以![]()
①当m≤0时,![]() ,则g(x)在(0,1]上单调递减,所以
,则g(x)在(0,1]上单调递减,所以![]()
②当0<m≤2时,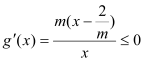 ,则g(x)在(0,1]上单调递减,
,则g(x)在(0,1]上单调递减,
所以![]()
③当m>2时,则![]() 时,
时,![]() 时,
时,![]()
所以g(x)在(0,![]() )上单调递减,在(
)上单调递减,在(![]() ,1]上单调递增,
,1]上单调递增,
故当![]() 时,g(x)取最小值为g(
时,g(x)取最小值为g(![]() ).
).
因为g(![]() )<g(1)=0,所以
)<g(1)=0,所以![]()
综上所述,存在m满足题意,其取值范围为(-∞,2].
-
科目: 来源: 题型:
查看答案和解析>>【题目】设数列
 的前
的前 项和为
项和为 ,
, 。
。(1)求证:数列
 为等差数列,并分别写出
为等差数列,并分别写出 和
和 关于
关于 的表达式;
的表达式;(2)是否存在自然数
 ,使得
,使得 ?若存在,求出
?若存在,求出 的值;来若不存在,请说明理由。
的值;来若不存在,请说明理由。(3)设
 ,
,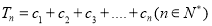 ,若不等式
,若不等式 对
对 恒成立,求
恒成立,求 的最大值。
的最大值。 -
科目: 来源: 题型:
查看答案和解析>>【题目】一房产商竞标得一块扇形
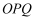 地皮,其圆心角
地皮,其圆心角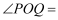
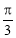 ,半径为
,半径为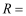
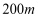 ,房产商欲在此地皮上修建一栋平面图为矩形的商住楼,为使得地皮的使用率最大,准备了两种设计方案如图,方案一:矩形
,房产商欲在此地皮上修建一栋平面图为矩形的商住楼,为使得地皮的使用率最大,准备了两种设计方案如图,方案一:矩形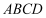 的一边
的一边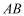 在半径
在半径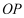 上,
上, 在圆弧上,
在圆弧上,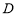 在半径
在半径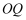 ;方案二:矩形EFGH的顶点在圆弧上,顶点
;方案二:矩形EFGH的顶点在圆弧上,顶点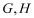 分别在两条半径上。请你通过计算,为房产商提供决策建议。
分别在两条半径上。请你通过计算,为房产商提供决策建议。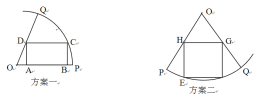
-
科目: 来源: 题型:
查看答案和解析>>【题目】4个不同的球,4个不同的盒子,把球全部放入盒内.
(1)恰有1个盒不放球,共有几种放法?
(2)恰有1个盒内有2个球,共有几种放法?
(3)恰有2个盒不放球,共有几种放法?
-
科目: 来源: 题型:
查看答案和解析>>【题目】函数

 (
( 满足:
满足:(1)
 ,
,(2)在区间
 内有最大值无最小值,
内有最大值无最小值,(3)在区间
 内有最小值无最大值,
内有最小值无最大值,(4)经过
 。
。(1)求
 的解析式;
的解析式;(2)若
 ,求
,求 值;
值;(3)不等式
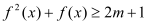 的解集不为空集,求实数
的解集不为空集,求实数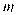 的范围.
的范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知两圆
 ,
, 的圆心分别为c1,c2,,P为一个动点,且
的圆心分别为c1,c2,,P为一个动点,且 .
.(1)求动点P的轨迹方程;
(2)是否存在过点A(2,0)的直线l与轨迹M交于不同的两点C,D,使得C1C=C1D?若存在,求出直线l的方程;若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,把两个全等的
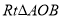 和
和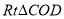 分别置于平面直角坐标系中,使直角边
分别置于平面直角坐标系中,使直角边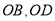 在
在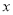 轴上,已知点
轴上,已知点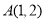 ,过
,过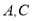 两点的直线分别交
两点的直线分别交 轴、
轴、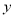 轴于点
轴于点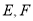 . 抛物线
. 抛物线 经过
经过 三点.
三点.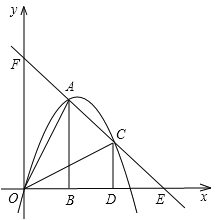
(1)求该抛物线的函数解析式;
(2)点
 为线段
为线段 上的一个动点,过点
上的一个动点,过点 作
作 轴的平行线交抛物线于点
轴的平行线交抛物线于点 ,交
,交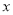 轴于点
轴于点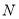 ,问是否存在这样的点
,问是否存在这样的点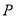 ,使得四边形
,使得四边形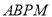 为等腰梯形?若存在,求出此时点
为等腰梯形?若存在,求出此时点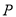 的坐标;若不存在,请说明理由;
的坐标;若不存在,请说明理由;(3)若
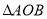 沿
沿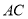 方向平移(点
方向平移(点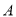 始终在线段
始终在线段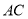 上,且不与点
上,且不与点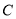 重合),
重合),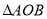 在平移的过程中与
在平移的过程中与 重叠部分的面积记为
重叠部分的面积记为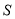 ,试探究
,试探究 是否存在最大值?若存在,求出这个最大值;若不存在,请说明理由.
是否存在最大值?若存在,求出这个最大值;若不存在,请说明理由.
相关试题

