【题目】函数![]()
![]() (
(![]() 满足:
满足:
(1)![]() ,
,
(2)在区间![]() 内有最大值无最小值,
内有最大值无最小值,
(3)在区间![]() 内有最小值无最大值,
内有最小值无最大值,
(4)经过![]() 。
。
(1)求![]() 的解析式;
的解析式;
(2)若![]() ,求
,求![]() 值;
值;
(3)不等式![]() 的解集不为空集,求实数
的解集不为空集,求实数![]() 的范围.
的范围.
参考答案:
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() .
.
【解析】
试题分析:(1)根据函数的对称性,可得函数的对称轴是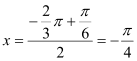 ,以及
,以及 ,再根据条件(2)(3)可得
,再根据条件(2)(3)可得![]() 在
在![]() 处取得最大值,在
处取得最大值,在![]() 处取得最小值,这样可知道函数的周期
处取得最小值,这样可知道函数的周期![]() 根据五点法求
根据五点法求![]() ,根据条件(4)求A;(2)代入可求得
,根据条件(4)求A;(2)代入可求得![]() ,因为
,因为![]() ,这样
,这样![]() ,根据同角基本关系求解;(3)将问题转化为
,根据同角基本关系求解;(3)将问题转化为![]() (其中
(其中![]() ),
),![]() ,即可解得
,即可解得![]() 的取值范围.
的取值范围.
试题解析:(1)由条件(1)(2)(3)可知,![]() 和
和![]() 为相邻对称轴,且
为相邻对称轴,且![]() 在
在![]() 处取得最大值,在
处取得最大值,在![]() 处取得最小值.
处取得最小值.
所以![]() 得
得![]() ;由
;由![]() 在
在![]() 处取得最大值得
处取得最大值得![]() 且
且![]() 。
。
经过![]() ,所以
,所以![]() ,解得
,解得![]()
所以![]()
![]()
(2)因为![]() ,所以
,所以![]() ;
;
![]()
(3)![]() (其中
(其中![]() )
)
![]()
![]()
![]() ,所以
,所以![]()
![]() ,解得:
,解得:
-
科目: 来源: 题型:
查看答案和解析>>【题目】一房产商竞标得一块扇形
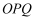 地皮,其圆心角
地皮,其圆心角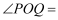
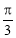 ,半径为
,半径为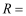
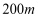 ,房产商欲在此地皮上修建一栋平面图为矩形的商住楼,为使得地皮的使用率最大,准备了两种设计方案如图,方案一:矩形
,房产商欲在此地皮上修建一栋平面图为矩形的商住楼,为使得地皮的使用率最大,准备了两种设计方案如图,方案一:矩形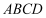 的一边
的一边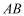 在半径
在半径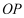 上,
上, 在圆弧上,
在圆弧上,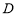 在半径
在半径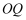 ;方案二:矩形EFGH的顶点在圆弧上,顶点
;方案二:矩形EFGH的顶点在圆弧上,顶点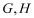 分别在两条半径上。请你通过计算,为房产商提供决策建议。
分别在两条半径上。请你通过计算,为房产商提供决策建议。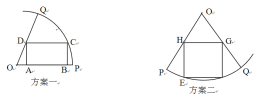
-
科目: 来源: 题型:
查看答案和解析>>【题目】4个不同的球,4个不同的盒子,把球全部放入盒内.
(1)恰有1个盒不放球,共有几种放法?
(2)恰有1个盒内有2个球,共有几种放法?
(3)恰有2个盒不放球,共有几种放法?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 在点(1,f(1))处的切线为y=1.
在点(1,f(1))处的切线为y=1.(1)求a,b的值;
(2)问是否存在实数m,使得当x∈(0,1]时,
 的最小值为0?若存在求出m的取值范围;若不存在,请说明理由.
的最小值为0?若存在求出m的取值范围;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知两圆
 ,
, 的圆心分别为c1,c2,,P为一个动点,且
的圆心分别为c1,c2,,P为一个动点,且 .
.(1)求动点P的轨迹方程;
(2)是否存在过点A(2,0)的直线l与轨迹M交于不同的两点C,D,使得C1C=C1D?若存在,求出直线l的方程;若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,把两个全等的
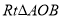 和
和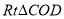 分别置于平面直角坐标系中,使直角边
分别置于平面直角坐标系中,使直角边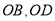 在
在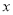 轴上,已知点
轴上,已知点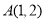 ,过
,过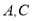 两点的直线分别交
两点的直线分别交 轴、
轴、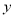 轴于点
轴于点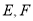 . 抛物线
. 抛物线 经过
经过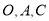 三点.
三点.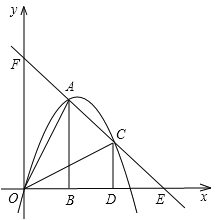
(1)求该抛物线的函数解析式;
(2)点
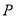 为线段
为线段 上的一个动点,过点
上的一个动点,过点 作
作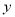 轴的平行线交抛物线于点
轴的平行线交抛物线于点 ,交
,交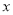 轴于点
轴于点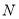 ,问是否存在这样的点
,问是否存在这样的点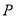 ,使得四边形
,使得四边形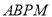 为等腰梯形?若存在,求出此时点
为等腰梯形?若存在,求出此时点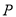 的坐标;若不存在,请说明理由;
的坐标;若不存在,请说明理由;(3)若
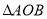 沿
沿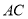 方向平移(点
方向平移(点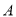 始终在线段
始终在线段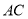 上,且不与点
上,且不与点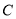 重合),
重合),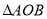 在平移的过程中与
在平移的过程中与 重叠部分的面积记为
重叠部分的面积记为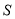 ,试探究
,试探究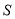 是否存在最大值?若存在,求出这个最大值;若不存在,请说明理由.
是否存在最大值?若存在,求出这个最大值;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】大学毕业生小王相应国家“自主创业”的号召,利用银行小额无息贷款开办了一家饰品店,该店购进一种今年新上市的饰品进行销售,饰品的进价为每件40元,售价为每件60元,每月可卖出300件,市场调查反映:调整价格时,售价每涨1元每月要少卖10件;售价每下降1元每月多卖20件,为获得更大的利润,现将饰品售价调整为
 (元/件)(
(元/件)( 即售价上涨,
即售价上涨, 即售价下降),每月饰品销售为
即售价下降),每月饰品销售为 (件),月利润为
(件),月利润为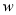 (元).
(元).(1)直接写出
 与
与 之间的函数关系式;
之间的函数关系式;(2)如何确定销售价格才能使月利润最大?求最大月利润;
(3)为了使每月利润不少于6000元,应如何控制销售价格?
相关试题

