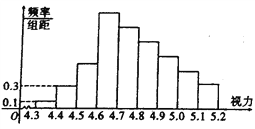
【题目】统计全国高三学生的视力情况,得到如图所示的频率分布直方图,由于不慎将部分数据丢失,但知道前4组的频率成等比数列,后6组的频率成等差数列.
(Ⅰ)求出视力在[4.7,4.8]的频率;
(Ⅱ)现从全国的高三学生中随机地抽取4人,用![]() 表示视力在[4.3,4.7]的学生人数,写出
表示视力在[4.3,4.7]的学生人数,写出![]() 的分布列,并求出
的分布列,并求出![]() 的期望与方差.
的期望与方差.
参考答案:
【答案】(1)![]() (2)见解析
(2)见解析
【解析】试题分析:(Ⅰ)结合频率分布直方图和题意,分别求出前4组的频率以及后6组的频率之和,由等差数列前n项和公式,求出公差,再算出视力在[4.7,4.8]内的频率;(Ⅱ)求出视力在[4.3,4.7]内的频率,学生人数![]() 服从二项分布
服从二项分布![]() ,由二项分布的概率计算公式求出分布列,再算出期望与方差.
,由二项分布的概率计算公式求出分布列,再算出期望与方差.
试题解析:(Ⅰ)前四组的频率分别为:0.01,0.03,0.09,0.27,所以后六组数据的首项为0.27,后六组的频率之和为![]() ,
,
设公差为![]() ,则有:
,则有: ![]()
![]() ,
,
所以,视力在[4.7,4.8]的频率![]() .
.
(Ⅱ)视力在[4.3,4.7]的频率为: ![]() ,
, ![]() ,
,
![]() ,
,
![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
,
![]() ,
,
所以![]() 的分布列为:
的分布列为:
| 0 | 1 | 2 | 3 | 4 |
|
|
|
|
|
|
![]() ,
,
![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四棱锥S﹣ABCD中,△ABD是正三角形,CB=CD,SC⊥BD.
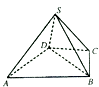
(Ⅰ)求证:SB=SD;
(Ⅱ)若∠BCD=120°,M为棱SA的中点,求证:DM∥平面SBC. -
科目: 来源: 题型:
查看答案和解析>>【题目】在定义域内既是奇函数又是减函数的是( )
A.y=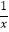
B.y=﹣x+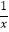
C.y=﹣x|x|
D.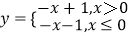
-
科目: 来源: 题型:
查看答案和解析>>【题目】若函数f(x)=x2+2(a﹣1)x+2在区间[﹣1,2]上单调,则实数a的取值范围为( )
A.[2,+∞)
B.(﹣∞,﹣1]
C.(﹣∞,﹣1]∪[2,+∞)
D.(﹣∞,﹣1)∪(2,+∞) -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=1﹣
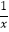 (x>0),若存在实数a,b(a<b),使y=f(x)的定义域为(a,b)时,值域为(ma,mb),则实数m的取值范围是( )
(x>0),若存在实数a,b(a<b),使y=f(x)的定义域为(a,b)时,值域为(ma,mb),则实数m的取值范围是( )
A.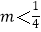
B.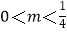
C.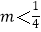 且m≠0
且m≠0
D.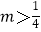
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知集合A={x|x2﹣3x+2=0},B={x|x2﹣mx+2=0},且A∩B=B,求实数m的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】选修4-4:坐标系与参数方程
已知圆
 和直线
和直线 .
.(Ⅰ)求
 的参数方程以及圆
的参数方程以及圆 上距离直线
上距离直线 最远的点
最远的点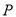 坐标;
坐标;(Ⅱ)以坐标原点
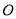 为极点,
为极点,  轴正半轴为极轴建立极坐标系,将圆
轴正半轴为极轴建立极坐标系,将圆 上除点
上除点 以外所有点绕着
以外所有点绕着 逆时针旋转
逆时针旋转 得到曲线
得到曲线 ,求曲线
,求曲线 的极坐标方程.
的极坐标方程.
相关试题

