【题目】若函数f(x)=x2+2(a﹣1)x+2在区间[﹣1,2]上单调,则实数a的取值范围为( )
A.[2,+∞)
B.(﹣∞,﹣1]
C.(﹣∞,﹣1]∪[2,+∞)
D.(﹣∞,﹣1)∪(2,+∞)
参考答案:
【答案】C
【解析】解:∵函数f(x)=x2+2(a﹣1)x+2的图象是开口方向朝上,且以x=﹣a﹣1为对称轴的抛物线,
∴函数f(x)=x2+2(a﹣1)x+2在区间(﹣∞,﹣a+1]上是减函数,在区间[﹣a+1,+∞)上是增函数,
∵函数f(x)=x2+2(a﹣1)x+2在区间[﹣1,2]上是单调函数,
∴﹣a+1≤﹣1,或﹣a+1≥2,
解得a≥2或a≤﹣1.
故选:C.
【考点精析】认真审题,首先需要了解二次函数的性质(当![]() 时,抛物线开口向上,函数在
时,抛物线开口向上,函数在![]() 上递减,在
上递减,在![]() 上递增;当
上递增;当![]() 时,抛物线开口向下,函数在
时,抛物线开口向下,函数在![]() 上递增,在
上递增,在![]() 上递减).
上递减).
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知f(x)=ax2+x﹣a,a∈R
(1)若a=1,解不等式f(x)≥1;
(2)若a<0,解不等式f(x)>1. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四棱锥S﹣ABCD中,△ABD是正三角形,CB=CD,SC⊥BD.
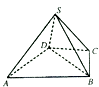
(Ⅰ)求证:SB=SD;
(Ⅱ)若∠BCD=120°,M为棱SA的中点,求证:DM∥平面SBC. -
科目: 来源: 题型:
查看答案和解析>>【题目】在定义域内既是奇函数又是减函数的是( )
A.y=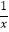
B.y=﹣x+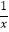
C.y=﹣x|x|
D.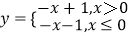
-
科目: 来源: 题型:
查看答案和解析>>【题目】统计全国高三学生的视力情况,得到如图所示的频率分布直方图,由于不慎将部分数据丢失,但知道前4组的频率成等比数列,后6组的频率成等差数列.
(Ⅰ)求出视力在[4.7,4.8]的频率;
(Ⅱ)现从全国的高三学生中随机地抽取4人,用
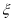 表示视力在[4.3,4.7]的学生人数,写出
表示视力在[4.3,4.7]的学生人数,写出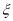 的分布列,并求出
的分布列,并求出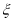 的期望与方差.
的期望与方差.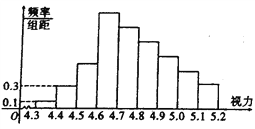
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=1﹣
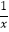 (x>0),若存在实数a,b(a<b),使y=f(x)的定义域为(a,b)时,值域为(ma,mb),则实数m的取值范围是( )
(x>0),若存在实数a,b(a<b),使y=f(x)的定义域为(a,b)时,值域为(ma,mb),则实数m的取值范围是( )
A.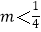
B.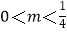
C.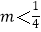 且m≠0
且m≠0
D.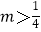
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知集合A={x|x2﹣3x+2=0},B={x|x2﹣mx+2=0},且A∩B=B,求实数m的取值范围.
相关试题

