【题目】已知下图中,四边形 ABCD是等腰梯形, ![]() ,
, ![]() ,
, ![]() 于M、交EF于点N,
于M、交EF于点N, ![]() ,
, ![]() ,现将梯形ABCD沿EF折起,记折起后C、D为
,现将梯形ABCD沿EF折起,记折起后C、D为![]() 、
、![]() 且使
且使![]() ,如图示.
,如图示.
![]()
![]()

(Ⅰ)证明: ![]()
![]() 平面ABFE;,
平面ABFE;,
(Ⅱ)若图6中, ![]() ,求点M到平面
,求点M到平面![]() 的距离.
的距离.
参考答案:
【答案】 (Ⅰ)见解析 (Ⅱ) ![]() .
.
【解析】试题分析:(I)折叠前后, ![]() ⊥EF、MN⊥EF,故EF⊥平面
⊥EF、MN⊥EF,故EF⊥平面![]() ,故
,故![]() .利用勾股定理可证得
.利用勾股定理可证得![]() ,所以
,所以![]()
![]() 平面ABFE;(II)设点M到平面
平面ABFE;(II)设点M到平面![]() 的距离为h,
的距离为h, ![]() ,
, ![]() ,利用勾股定理证明
,利用勾股定理证明![]() ,利用等体积法可求得点M到平面
,利用等体积法可求得点M到平面![]() 的距离为
的距离为![]() .
.
试题解析:
(Ⅰ) 可知![]() ,∴
,∴![]() ⊥EF、MN⊥EF,
⊥EF、MN⊥EF,

又![]() ,得EF⊥平面
,得EF⊥平面![]() ,
,
得![]() ,
,
∵![]() ∴
∴![]() ,
,
又![]() ,∴
,∴![]()
![]() 平面ABFE.
平面ABFE.
(Ⅱ) 设点M到平面![]() 的距离为h,
的距离为h,
由![]() ,得
,得![]() ,①
,①
∵![]() ,
, ![]() ,
,
∴![]() ,
, ![]() ,
,
在![]() 中,
中, ![]() ,
,
又![]() ,
, ![]() ,得
,得![]() ,
,
∴![]() ,
,
![]() ,又
,又![]() ,
,
代入①式,得![]() ,解得
,解得![]() ,
,
∴点M到平面![]() 的距离为
的距离为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】选修4
 4:坐标系与参数方程
4:坐标系与参数方程在直角坐标系
 中,已知直线l1:
中,已知直线l1:  (
( ,
,  ),抛物线C:
),抛物线C:  (t为参数).以原点
(t为参数).以原点 为极点,
为极点,  轴的非负半轴为极轴建立极坐标系.
轴的非负半轴为极轴建立极坐标系.(Ⅰ)求直线l1 和抛物线C的极坐标方程;
(Ⅱ)若直线l1 和抛物线C相交于点A(异于原点O),过原点作与l1垂直的直线l2,l2和抛物线C相交于点B(异于原点O),求△OAB的面积的最小值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
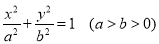 与抛物线
与抛物线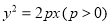 共焦点
共焦点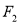 ,抛物线上的点M到y轴的距离等于
,抛物线上的点M到y轴的距离等于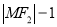 ,且椭圆与抛物线的交点Q满足
,且椭圆与抛物线的交点Q满足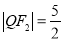 .
.(I)求抛物线的方程和椭圆的方程;
(II)过抛物线上的点
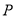 作抛物线的切线
作抛物线的切线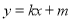 交椭圆于
交椭圆于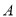 、
、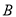 两点,求此切线在x轴上的截距的取值范围.
两点,求此切线在x轴上的截距的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】某学校在一次第二课堂活动中,特意设置了过关智力游戏,游戏共五关.规定第一关没过者没奖励,过
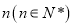 关者奖励
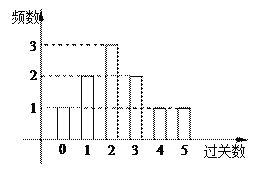
关者奖励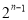 件小奖品(奖品都一样).下图是小明在10次过关游戏中过关数的条形图,以此频率估计概率.
件小奖品(奖品都一样).下图是小明在10次过关游戏中过关数的条形图,以此频率估计概率.(Ⅰ)求小明在这十次游戏中所得奖品数的均值;
(Ⅱ)规定过三关者才能玩另一个高级别的游戏,估计小明一次游戏后能玩另一个游戏的概率;
(Ⅲ)已知小明在某四次游戏中所过关数为{2,2,3,4},小聪在某四次游戏中所过关数为{3,3,4,5},现从中各选一次游戏,求小明和小聪所得奖品总数超过10的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】设函数
 (
( ),
), ,
,(Ⅰ) 试求曲线
 在点
在点 处的切线l与曲线
处的切线l与曲线 的公共点个数;(Ⅱ) 若函数
的公共点个数;(Ⅱ) 若函数 有两个极值点,求实数a的取值范围.
有两个极值点,求实数a的取值范围.(附:当
 ,x趋近于0时,
,x趋近于0时,  趋向于
趋向于 )
) -
科目: 来源: 题型:
查看答案和解析>>【题目】《九章算术》中有这样一则问题:“今有良马与弩马发长安,至齐,齐去长安三千里,良马初日行一百九十三里,日增一十三里;弩马初日行九十七里,日减半里,良马先至齐,复还迎弩马.”则现有如下说法:
①弩马第九日走了九十三里路;
②良马前五日共走了一千零九十五里路;
③良马和弩马相遇时,良马走了二十一日.
则以上说法错误的个数是( )个
A. 0 B. 1 C. 2 D. 3
-
科目: 来源: 题型:
查看答案和解析>>【题目】某玩具生产公司每天计划生产卫兵、骑兵、伞兵这三种玩具共
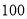 个,生产一个卫兵需
个,生产一个卫兵需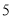 分钟,生产一个骑兵需
分钟,生产一个骑兵需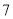 分钟,生产一个伞兵需
分钟,生产一个伞兵需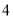 分钟,已知总生产时间不超过
分钟,已知总生产时间不超过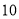 小时,若生产一个卫兵可获利润
小时,若生产一个卫兵可获利润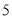 元,生产一个骑兵可获利润
元,生产一个骑兵可获利润 元,生产一个伞兵可获利润
元,生产一个伞兵可获利润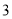 元.
元.(1)用每天生产的卫兵个数
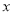 与骑兵个数
与骑兵个数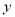 表示每天的利润
表示每天的利润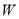 (元);
(元);(2)怎么分配生产任务才能使每天的利润最大,最大利润是多少?
相关试题

