【题目】已知函数 ![]() ,
, ![]()
(1)求函数的图象在点 ![]() 处的切线方程;
处的切线方程;
(2)当 ![]() 时,求证:
时,求证: ![]() ;
;
(3)若 ![]() 对任意的
对任意的 ![]() 恒成立,求实数
恒成立,求实数 ![]() 的取值范围.
的取值范围.
参考答案:
【答案】
(1)解: ![]() ,所以
,所以 ![]() ,切点为(0,0) ∴切线为y=x
,切点为(0,0) ∴切线为y=x
(2)解:证明:令g(x)= f(x)+x2-x= ex-x-1 ,g(x)= ex-1=0 ∴x=0
所以x ![]() (-∞,0)时,g(x)<0, g(x)单调递减.x
(-∞,0)时,g(x)<0, g(x)单调递减.x ![]() (0,+∞)时,g(x)>0, g(x)单调递增
(0,+∞)时,g(x)>0, g(x)单调递增
∴g(x)min= g(0)=0 ∴g(x) ![]() 0 ∴f(x)
0 ∴f(x) ![]() -x2+x
-x2+x
(3)解:f(x) ![]() kx对任意的x
kx对任意的x ![]() (0,+ ∞)恒成立等价于k<
(0,+ ∞)恒成立等价于k< ![]() 对任意的x
对任意的x ![]() (0,+ ∞)恒成立
(0,+ ∞)恒成立
令h(x)= ![]() , ∴h(x)=
, ∴h(x)= ![]() 由(2)知x
由(2)知x ![]() (0,+ ∞)时ex-x-1>0
(0,+ ∞)时ex-x-1>0
∴x ![]() (0,1)时h(x)<0, (x)单调递减,x
(0,1)时h(x)<0, (x)单调递减,x ![]() (1,+ ∞)时h(x)>0, h(x)单调递增
(1,+ ∞)时h(x)>0, h(x)单调递增
∴h(x)min=h(1)=e-2 ∴k<e-2 ∴k的取值范围(-∞,e-2)
【解析】(1)求出原函数的导函数,得出 f ' ( 0 ) = 1 再求出f(0),由直线方程的点斜式得出结果。(2)根据题意构造 g(x) 对其求导,令导数值等于零求出极点进而可得出 g(x) 的单调性故可求出最小值,即可得证。(3)分离出k得到k与x的关系式![]() ,利用导数求出 g(x) 的最小值即可得到k<e-2。
,利用导数求出 g(x) 的最小值即可得到k<e-2。
【考点精析】本题主要考查了利用导数研究函数的单调性和函数的极值与导数的相关知识点,需要掌握一般的,函数的单调性与其导数的正负有如下关系: 在某个区间![]() 内,(1)如果
内,(1)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递增;(2)如果
在这个区间单调递增;(2)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递减;求函数
在这个区间单调递减;求函数![]() 的极值的方法是:(1)如果在
的极值的方法是:(1)如果在![]() 附近的左侧
附近的左侧![]() ,右侧
,右侧![]() ,那么
,那么![]() 是极大值(2)如果在
是极大值(2)如果在![]() 附近的左侧
附近的左侧![]() ,右侧
,右侧![]() ,那么
,那么![]() 是极小值才能正确解答此题.
是极小值才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 .
.(1)解不等式
 ;
;(2)若函数
 在区间
在区间 上存在零点,求实数
上存在零点,求实数 的取值范围;
的取值范围;(3)若函数
 ,其中
,其中 为奇函数,
为奇函数,  为偶函数,若不等式
为偶函数,若不等式 对任意
对任意 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知定义在
 上的函数
上的函数 是奇函数.
是奇函数.(1)求
 的值;
的值;(2)判断
 的单调性,并用单调性定义证明;
的单调性,并用单调性定义证明;(3)若对任意的
 ,不等式
,不等式 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】某厂商为了解用户对其产品是否满意,在使用产品的用户中随机调查了80人,结果如下表:

(1)根据上述,现用分层抽样的方法抽取对产品满意的用户5人,在这5人中任选2人,求被选中的恰好是男、女用户各1人的概率;
(2)有多大把握认为用户对该产品是否满意与用户性别有关?请说明理由.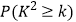
0.15
0.10
0.05
0.025
0.010
0.005
0.001
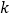
2.072
2.706
3.841
5.024
6.635
7.879
10.828
注:
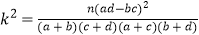
-
科目: 来源: 题型:
查看答案和解析>>【题目】在直角坐标系
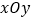 中,曲线
中,曲线 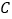 的方程为
的方程为 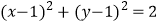 ,直线
,直线 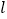 的倾斜角为
的倾斜角为 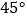 且经过点
且经过点 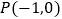 .
.
(1)以 为极点,
为极点, 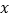 轴的正半轴为极轴建立极坐标系,求曲线
轴的正半轴为极轴建立极坐标系,求曲线 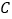 的极坐标方程;
的极坐标方程;
(2)设直线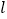 与曲线
与曲线 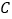 交于两点
交于两点 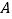 ,
, 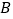 ,求
,求 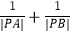 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知定义在R的函数
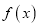 是偶函数,且满足
是偶函数,且满足 上的解析式为
上的解析式为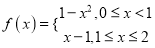 ,过点
,过点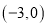 作斜率为k的直线l,若直线l与函数
作斜率为k的直线l,若直线l与函数 的图象至少有4个公共点,则实数k的取值范围是
的图象至少有4个公共点,则实数k的取值范围是A.
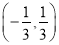 B.
B. 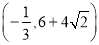 C.
C. 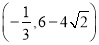 D.
D. 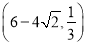
-
科目: 来源: 题型:
查看答案和解析>>【题目】十二生肖,又叫属相,是中国与十二地支相配以人出生年份的十二种动物,包括鼠、牛、虎、兔、龙、蛇、马、羊、猴、鸡、狗、猪。已知在甲、乙、丙、丁、戊、己六人中,甲、乙、丙的属相均是龙,丁、戊的属相均是虎,己的属相是猴,现从这六人中随机选出三人,则所选出的三人的属相互不相同的概率等于( )
A.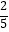
B.
C.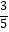
D.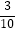
相关试题

