【题目】质监部门从某超市销售的甲、乙两种食用油中分别各随机抽取100桶检测某项质量指标,由检测结果得到如下的频率分布直方图:
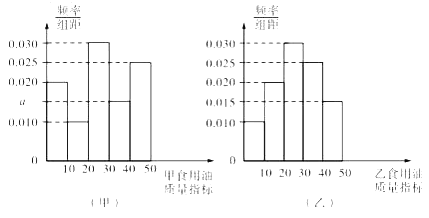
(Ⅰ)写出频率分布直方图(甲)中![]() 的值;记甲、乙两种食用油100桶样本的质量指标的方差分别为
的值;记甲、乙两种食用油100桶样本的质量指标的方差分别为![]() ,
,![]() ,试比较
,试比较![]() ,
,![]() 的大小(只要求写出答案);
的大小(只要求写出答案);
(Ⅱ)估计在甲、乙两种食用油中随机抽取1捅,恰有一桶的质量指标大于20;
(Ⅲ)由频率分布直方图可以认为,乙种食用油的质量指标值![]() 服从正态分布
服从正态分布![]() .其中
.其中![]() 近似为样本平均数
近似为样本平均数![]() ,
,![]() 近似为样本方差
近似为样本方差![]() ,设
,设![]() 表示从乙种食用油中随机抽取10桶,其质量指标值位于(14.55,38.45)的桶数,求
表示从乙种食用油中随机抽取10桶,其质量指标值位于(14.55,38.45)的桶数,求![]() 的数学期望.
的数学期望.
注:①同一组数据用该区问的中点值作代表,计算得![]()
②若![]()
![]() ,则
,则![]() ,
,![]() .
.
参考答案:
【答案】(1)![]() ,
,![]() .(2)
.(2)![]() (3)
(3)![]()
【解析】试题分析:(Ⅰ)根据频率之和为1,即小矩形的面积为1计算![]() 的值,根据图象判断乙的分布比较集中,方差小,甲波动大,方差大;(Ⅱ)根据频率分布直方图分布计算甲和乙两种食用油质量指标小于等于20的频率,和大于20的频率,将所求事件分为两种情况求概率;(Ⅲ)所求事件的概率为
的值,根据图象判断乙的分布比较集中,方差小,甲波动大,方差大;(Ⅱ)根据频率分布直方图分布计算甲和乙两种食用油质量指标小于等于20的频率,和大于20的频率,将所求事件分为两种情况求概率;(Ⅲ)所求事件的概率为![]()
![]() ,
, ![]() ,根据二项分布求期望.
,根据二项分布求期望.
试题解析:(Ⅰ)![]() ,
,![]() .
.
(Ⅱ)设事件![]() :在甲种食用油中随机抽取1桶,其质量指标不大于20,
:在甲种食用油中随机抽取1桶,其质量指标不大于20,
事件![]() :在乙种食用油中随机抽取1桶,其质量指标不大于20,
:在乙种食用油中随机抽取1桶,其质量指标不大于20,
事件![]() :在甲、乙两种食用油中随机抽取1桶,恰有一个桶的质量指标不大于20,且另一个不大于20,
:在甲、乙两种食用油中随机抽取1桶,恰有一个桶的质量指标不大于20,且另一个不大于20,
则![]() ,
,![]() ,
,
∴![]()
![]() ,
,
(Ⅲ)计算得:![]() ,由条件得
,由条件得![]() ,
,
从而![]() ,
,
∴从乙种食用油中随机抽取10桶,其质量指标值位于(14.55,38.45)的概率是0.6826,
根据题意得![]() ,
,
∴![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在菱形
 中,
中,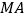 ⊥平面
⊥平面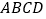 ,且四边形
,且四边形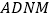 是平行四边形.
是平行四边形.
(1)求证:
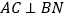 ;
;(2)当点
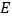 在
在 的什么位置时,使得
的什么位置时,使得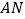 ∥平面
∥平面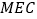 ,并加以证明.
,并加以证明. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形
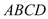 是梯形.四边形
是梯形.四边形 是矩形.且平面
是矩形.且平面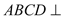 平面
平面 ,
,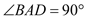 ,
,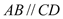 ,
, ,
,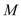 是线段
是线段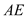 上的动点.
上的动点.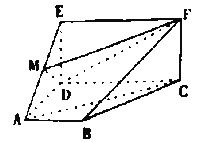
(Ⅰ)试确定点
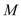 的位置,使
的位置,使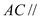 平面
平面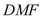 ,并说明理由;
,并说明理由;(Ⅱ)在(Ⅰ)的条件下,求平面
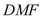 与平面
与平面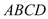 所成锐二面角的余弦值.
所成锐二面角的余弦值. -
科目: 来源: 题型:
查看答案和解析>>【题目】在等比数列
 中,
中, 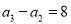 ,且
,且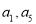 的等比中项为
的等比中项为 .
.(1)求数列
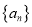 的通项公式;
的通项公式;(2)设
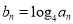 ,数列
,数列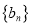 的前
的前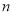 项和为
项和为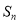 ,是否存在正整数
,是否存在正整数 ,使得
,使得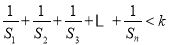 对任意
对任意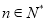 恒成立?若存在,求出正整数
恒成立?若存在,求出正整数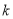 的最小值;若不存在,请说明理由.
的最小值;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】某算法的程序框图如图所示,其中输入的变量x在1,2,3,…,24这24个整数中等可能随机产生.
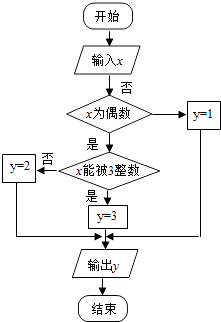
(1)分别求出按程序框图正确编程运行时输出y的值为i的概率Pi(i=1,2,3);
(2)甲、乙两同学依据自己对程序框图的理解,各自编写程序重复运行n次后,统计记录了输出y的值为i(i=1,2,3)的频数.以下是甲、乙所作频数统计表的部分数据.
甲的频数统计表(部分)运行
次数n输出y的值
为1的频数输出y的值
为2的频数输出y的值
为3的频数30
14
6
10
…
…
…
…
2100
1027
376
697
乙的频数统计表(部分)
运行
次数n输出y的值
为1的频数输出y的值
为2的频数输出y的值
为3的频数30
12
11
7
…
…
…
…
2100
1051
696
353
当n=2100时,根据表中的数据,分别写出甲、乙所编程序各自输出y的值为i(i=1,2,3)的频率(用分数表示),并判断两位同学中哪一位所编写程序符合算法要求的可能性较大.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一辆汽车从
 市出发沿海岸一条笔直公路以每小时
市出发沿海岸一条笔直公路以每小时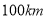 的速度向东均速行驶,汽车开动时,在
的速度向东均速行驶,汽车开动时,在 市南偏东方向距
市南偏东方向距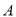 市
市 且与海岸距离为
且与海岸距离为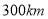 的海上
的海上 处有一快艇与汽车同时出发,要把一份稿件交给这汽车的司机.
处有一快艇与汽车同时出发,要把一份稿件交给这汽车的司机.(1)快艇至少以多大的速度行驶才能把稿件送到司机手中?
(2)在(1)的条件下,求快艇以最小速度行驶时的行驶方向与
 所成的角.
所成的角.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知
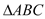 中,角
中,角 ,
,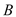 ,
,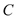 所对的边分别是
所对的边分别是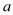 ,
,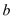 ,
,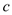 ,且点
,且点 ,
, ,动点
,动点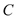 满足
满足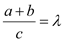 (
(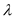 为常数且
为常数且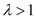 ),动点
),动点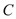 的轨迹为曲线
的轨迹为曲线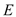 .
.(Ⅰ)试求曲线
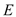 的方程;
的方程;(Ⅱ)当
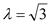 时,过定点
时,过定点 的直线与曲线
的直线与曲线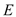 交于
交于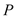 ,
,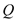 两点,
两点,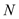 是曲线
是曲线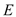 上不同于
上不同于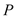 ,
,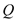 的动点,试求
的动点,试求 面积的最大值.
面积的最大值.
相关试题

