【题目】如图,四边形![]() 是梯形.四边形
是梯形.四边形![]() 是矩形.且平面
是矩形.且平面![]() 平面
平面![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 是线段
是线段![]() 上的动点.
上的动点.
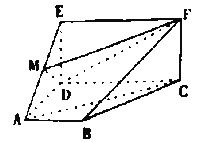
(Ⅰ)试确定点![]() 的位置,使
的位置,使![]() 平面
平面![]() ,并说明理由;
,并说明理由;
(Ⅱ)在(Ⅰ)的条件下,求平面![]() 与平面
与平面![]() 所成锐二面角的余弦值.
所成锐二面角的余弦值.
参考答案:
【答案】(1)见解析(2)![]()
【解析】试题分析:(Ⅰ)当点![]() 是中点时,连结
是中点时,连结![]() ,交
,交![]() 于点
于点![]() ,连结
,连结![]() ,根据中位线可知
,根据中位线可知![]() ,即
,即![]() 平面
平面![]() ;(Ⅱ)以点
;(Ⅱ)以点![]() 为原点建立空间直角坐标系,分别求两个平面
为原点建立空间直角坐标系,分别求两个平面![]() 的法向量
的法向量![]() ,求
,求![]() .
.
试题解析:(Ⅰ)当![]() 是
是![]() 线段的中点时,
线段的中点时,![]() 平面
平面![]() ,
,
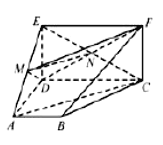
证明如下:
连接![]() ,交
,交![]() 于
于![]() ,连接
,连接![]() ,
,
由于![]() 、
、![]() 分别是
分别是![]() 、
、![]() 的中点,所以
的中点,所以![]() ,
,
由于![]() 平面
平面![]() ,又
,又![]() 不包含于平面
不包含于平面![]() ,
,
∴![]() 平面
平面![]() .
.
(Ⅱ)方法一:过点![]() 作平面
作平面![]() 与平面
与平面![]() 的交线
的交线![]() ,
,
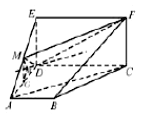
∵![]() 平面
平面![]() ,∴
,∴![]()
![]() ,
,
过点![]() 作
作![]() 于
于![]() ,
,
∵平面![]() 平面
平面![]() ,
,![]() ,
,
∴![]() 平面
平面![]() ,∴平面
,∴平面![]() 平面
平面![]() ,
,
∴![]() 平面
平面![]() ,
,
过![]() 作
作![]() 于
于![]() ,连接
,连接![]() ,则直线
,则直线![]() 平面
平面![]() ,∴
,∴![]() ,
,
设![]() ,则
,则![]() ,
,![]()
![]() ,
,![]() ,则
,则![]() ,
,
∴![]() ,
,
∴所求二面角的余弦值为![]() .
.
方法二:
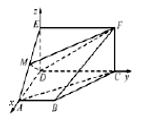
∵平面![]() 平面
平面![]() ,
,![]() ,
,
∴![]() 平面
平面![]() ,可知
,可知![]() 、
、![]() 、
、![]() 两两垂直,
两两垂直,
分别以![]() 、
、![]() 、
、![]() 的方向为
的方向为![]() ,
,![]() ,
,![]() 轴,
轴,
建立空间直角坐标系![]() .
.
设![]() ,则
,则![]() ,
,![]() ,
,![]() ,
,![]() ,
,
设平面![]() 的法向量
的法向量![]() ,
,
则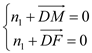 ,∴
,∴![]() ,
,
令![]() ,得平面
,得平面![]() 的一个法向量
的一个法向量![]() ,
,
取平面![]() 的法向量
的法向量![]() ,
,
由![]() ,
,
∴平面![]() 与平面
与平面![]() 所成锐二面角的余弦值为
所成锐二面角的余弦值为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
 :
: 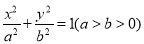 经过点
经过点 ,左右焦点分别为
,左右焦点分别为 、
、 ,圆
,圆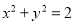 与直线
与直线 相交所得弦长为2.
相交所得弦长为2. (Ⅰ)求椭圆
 的标准方程;
的标准方程;(Ⅱ)设
 是椭圆
是椭圆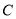 上不在
上不在 轴上的一个动点,
轴上的一个动点,  为坐标原点,过点
为坐标原点,过点 作
作 的平行线交椭圆
的平行线交椭圆 于
于 、
、 两个不同的点,求
两个不同的点,求 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】某食品厂为了检查甲、乙两条自动包装流水线的生产情况,随机在这两条流水线上各抽取40件产品作为样本,并称出它们的重量(单位:克),重量值落在
 内的产品为合格品,否则为不合格品,统计结果如表:
内的产品为合格品,否则为不合格品,统计结果如表: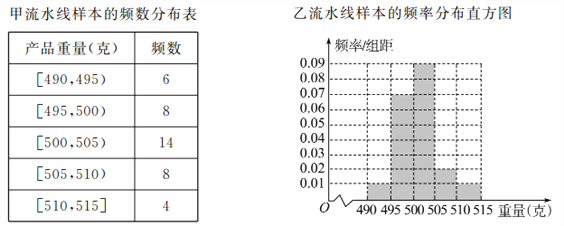
(Ⅰ)求甲流水线样本合格的频率;
(Ⅱ)从乙流水线上重量值落在
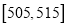 内的产品中任取2个产品,求这2件产品中恰好只有一件合格的概率.
内的产品中任取2个产品,求这2件产品中恰好只有一件合格的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在菱形
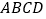 中,
中,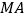 ⊥平面
⊥平面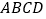 ,且四边形
,且四边形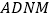 是平行四边形.
是平行四边形.
(1)求证:
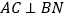 ;
;(2)当点
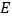 在
在 的什么位置时,使得
的什么位置时,使得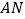 ∥平面
∥平面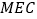 ,并加以证明.
,并加以证明. -
科目: 来源: 题型:
查看答案和解析>>【题目】在等比数列
 中,
中, 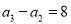 ,且
,且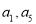 的等比中项为
的等比中项为 .
.(1)求数列
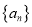 的通项公式;
的通项公式;(2)设
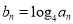 ,数列
,数列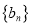 的前
的前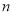 项和为
项和为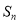 ,是否存在正整数
,是否存在正整数 ,使得
,使得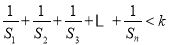 对任意
对任意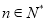 恒成立?若存在,求出正整数
恒成立?若存在,求出正整数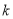 的最小值;若不存在,请说明理由.
的最小值;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】质监部门从某超市销售的甲、乙两种食用油中分别各随机抽取100桶检测某项质量指标,由检测结果得到如下的频率分布直方图:
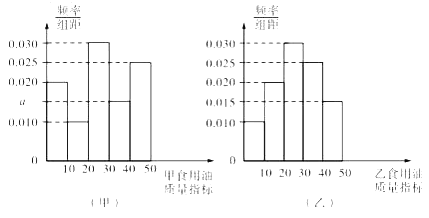
(Ⅰ)写出频率分布直方图(甲)中
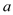 的值;记甲、乙两种食用油100桶样本的质量指标的方差分别为
的值;记甲、乙两种食用油100桶样本的质量指标的方差分别为 ,
,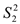 ,试比较
,试比较 ,
,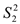 的大小(只要求写出答案);
的大小(只要求写出答案);(Ⅱ)估计在甲、乙两种食用油中随机抽取1捅,恰有一桶的质量指标大于20;
(Ⅲ)由频率分布直方图可以认为,乙种食用油的质量指标值
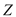 服从正态分布
服从正态分布 .其中
.其中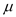 近似为样本平均数
近似为样本平均数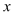 ,
,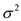 近似为样本方差
近似为样本方差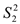 ,设
,设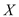 表示从乙种食用油中随机抽取10桶,其质量指标值位于(14.55,38.45)的桶数,求
表示从乙种食用油中随机抽取10桶,其质量指标值位于(14.55,38.45)的桶数,求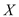 的数学期望.
的数学期望.注:①同一组数据用该区问的中点值作代表,计算得

②若
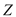
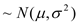 ,则
,则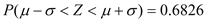 ,
,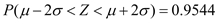 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】某算法的程序框图如图所示,其中输入的变量x在1,2,3,…,24这24个整数中等可能随机产生.
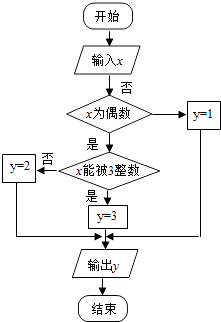
(1)分别求出按程序框图正确编程运行时输出y的值为i的概率Pi(i=1,2,3);
(2)甲、乙两同学依据自己对程序框图的理解,各自编写程序重复运行n次后,统计记录了输出y的值为i(i=1,2,3)的频数.以下是甲、乙所作频数统计表的部分数据.
甲的频数统计表(部分)运行
次数n输出y的值
为1的频数输出y的值
为2的频数输出y的值
为3的频数30
14
6
10
…
…
…
…
2100
1027
376
697
乙的频数统计表(部分)
运行
次数n输出y的值
为1的频数输出y的值
为2的频数输出y的值
为3的频数30
12
11
7
…
…
…
…
2100
1051
696
353
当n=2100时,根据表中的数据,分别写出甲、乙所编程序各自输出y的值为i(i=1,2,3)的频率(用分数表示),并判断两位同学中哪一位所编写程序符合算法要求的可能性较大.
相关试题

