【题目】已知函数![]() ,
,![]() .
.
(1)讨论![]() 的单调性;
的单调性;
(2)若![]() 有两个极值点
有两个极值点![]() ,
,![]() ,且
,且![]() ,证明:
,证明:![]() .
.
参考答案:
【答案】(1)见解析.(2)见解析.
【解析】分析:(1)先求导数,再根据二次方程![]() =0根得情况分类讨论:当
=0根得情况分类讨论:当![]() 时,
时,![]() .∴
.∴![]() 在
在![]() 上单调递减. 当
上单调递减. 当![]() 时,根据两根大小再分类讨论对应单调区间, (2)先化简不等式
时,根据两根大小再分类讨论对应单调区间, (2)先化简不等式![]() 消m得
消m得![]() ,再利用导数研究
,再利用导数研究![]() ,
,![]() 单调性,得其最小值大于-1,即证得结果.
单调性,得其最小值大于-1,即证得结果.
详解:(1)由![]() ,得
,得
![]()
![]() ,
,![]() .
.
设![]() ,
,![]() .
.
当![]() 时,即
时,即![]() 时,
时,![]() ,
,![]() .
.
∴![]() 在
在![]() 上单调递减.
上单调递减.
当![]() 时,即
时,即![]() 时,
时,
令![]() ,得
,得![]() ,
,![]() ,
,![]() .
.
当![]() 时,
时,![]() ,
,
在![]() 上,
上,![]() ,在
,在![]() 上,
上,![]() ,
,
∴![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减.
上单调递减.
综上,当![]() 时,
时,![]() 在
在![]() 上单调递减,
上单调递减,
当![]() 时,
时,![]() 在
在![]() ,
,![]() 上单调递减,在
上单调递减,在![]() 上单调递增,
上单调递增,
当![]() 时,
时,![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减.
上单调递减.
(2)∵![]() 有两个极值点
有两个极值点![]() ,
,![]() ,且
,且![]() ,
,
∴由(1)知![]() 有两个不同的零点
有两个不同的零点![]() ,
,![]() ,
,
![]() ,
,![]() ,且
,且![]() ,此时,
,此时,![]() ,
,
要证明![]() ,只要证明
,只要证明![]() .
.
∵![]() ,∴只要证明
,∴只要证明![]() 成立.
成立.
∵![]() ,∴
,∴![]() .
.
设![]() ,
,![]() ,
,
则![]() ,
,
当![]() 时,
时,![]() ,
,
∴![]() 在
在![]() 上单调递增,
上单调递增,
∴![]() ,即
,即![]() ,
,
∴![]() 有两个极值点
有两个极值点![]() ,
,![]() ,且
,且![]() 时,
时,![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】当x∈R,|x|<1时,有如下表达式:1+x+x2+…+xn+…=

两边同时积分得: dx+
dx+  xdx+
xdx+  x2dx+…+
x2dx+…+  xndx+…=
xndx+…= 
 dx
dx
从而得到如下等式:1× +
+  ×(
×(  )2+
)2+  ×(
×(  )3+…+
)3+…+  ×(
×(  )n+1+…=ln2
)n+1+…=ln2
请根据以上材料所蕴含的数学思想方法,计算: ×
×  +
+ 
 ×(
×(  )2+
)2+ 
 ×(
×(  )3+…+
)3+…+ 
 ×(
×(  )n+1= .
)n+1= . -
科目: 来源: 题型:
查看答案和解析>>【题目】我国古代著名的
 周髀算经
周髀算经 中提到:凡八节二十四气,气损益九寸九分六分分之一;冬至晷
中提到:凡八节二十四气,气损益九寸九分六分分之一;冬至晷 长一丈三尺五寸,夏至晷长一尺六寸
长一丈三尺五寸,夏至晷长一尺六寸 意思是:一年有二十四个节气,每相邻两个节气之间的日影长度差为
意思是:一年有二十四个节气,每相邻两个节气之间的日影长度差为 分;且“冬至”时日影长度最大,为1350分;“夏至”时日影长度最小,为160分
分;且“冬至”时日影长度最大,为1350分;“夏至”时日影长度最小,为160分 则“立春”时日影长度为
则“立春”时日影长度为


A.
 分B.
分B.  分C.
分C.  分D.
分D.  分
分 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知锐角
 的外接圆的半径为1,
的外接圆的半径为1, ,则
,则 的面积的取值范围为_____.
的面积的取值范围为_____. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,墙上有一壁画,最高点
 离地面4米,最低点
离地面4米,最低点 离地面2米,观察者从距离墙
离地面2米,观察者从距离墙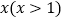 米,离地面高
米,离地面高 米的
米的 处观赏该壁画,设观赏视角
处观赏该壁画,设观赏视角

(1)若
 问:观察者离墙多远时,视角
问:观察者离墙多远时,视角 最大?
最大?(2)若
 当
当 变化时,求
变化时,求 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】求下列函数的值域:
(1)y=
 ;
; (2)y=
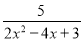 ;
;(3)y=x+4
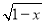 ;
;(4)y=
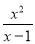 (x>1)
(x>1) -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 的图象如图所示,则下列说法正确的是( )
的图象如图所示,则下列说法正确的是( )
A. 函数
 的周期为
的周期为
B. 函数
 在
在 上单调递增
上单调递增C. 函数
 的图象关于点
的图象关于点 对称
对称D. 把函数
 的图象向右平移
的图象向右平移 个单位,所得图象对应的函数为奇函数
个单位,所得图象对应的函数为奇函数
相关试题

