【题目】求下列函数的值域:
(1)y=![]() ;
;
(2)y=![]() ;
;
(3)y=x+4![]() ;
;
(4)y=![]() (x>1)
(x>1)
参考答案:
【答案】(1) {y|y≠3};(2) (0,5];(3) (-∞,5];(4) [4,+∞).
【解析】
(1)根据分式函数的性质,利用分子常数化进行求解.(2)分母进行配方,利用一元二次函数以及分式函数的性质进行求解,(3)利用换元法转化为一元二次函数进行求解.(4)利用分式的性质,结合基本不等式的应用进行求解.
(1)y![]() 3
3![]() ,则y≠3,
,则y≠3,
即函数的值域为{y|y≠3};
(2)y![]() ,
,
∵2(x﹣1)2+1≥1,∴![]() ∈(0,5],即函数的值域为(0,5];
∈(0,5],即函数的值域为(0,5];
(3)由1﹣x≥0得x≤1,则函数的定义域为(﹣∞,1],
设t![]() ,则x=1﹣t2,t≥0,
,则x=1﹣t2,t≥0,
则y=x+4![]() 1﹣t2+4t=﹣(t﹣2)2+5,
1﹣t2+4t=﹣(t﹣2)2+5,
∵t≥0,∴y≤5,即函数的值域为(﹣∞,5]
(4)y![]() x﹣1
x﹣1![]() 2,
2,
∵x>1,∴x﹣1>0,
则y=x﹣1![]() 2≥2+2
2≥2+2![]() 2+2=4,
2+2=4,
当且仅当x﹣1![]() ,解集x﹣1=1,x=2时,取等号,
,解集x﹣1=1,x=2时,取等号,
故函数的值域为[4,+∞).
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知锐角
 的外接圆的半径为1,
的外接圆的半径为1, ,则
,则 的面积的取值范围为_____.
的面积的取值范围为_____. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 ,
, .
.(1)讨论
 的单调性;
的单调性;(2)若
 有两个极值点
有两个极值点 ,
, ,且
,且 ,证明:
,证明: .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,墙上有一壁画,最高点
 离地面4米,最低点
离地面4米,最低点 离地面2米,观察者从距离墙
离地面2米,观察者从距离墙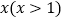 米,离地面高
米,离地面高 米的
米的 处观赏该壁画,设观赏视角
处观赏该壁画,设观赏视角

(1)若
 问:观察者离墙多远时,视角
问:观察者离墙多远时,视角 最大?
最大?(2)若
 当
当 变化时,求
变化时,求 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 的图象如图所示,则下列说法正确的是( )
的图象如图所示,则下列说法正确的是( )
A. 函数
 的周期为
的周期为
B. 函数
 在
在 上单调递增
上单调递增C. 函数
 的图象关于点
的图象关于点 对称
对称D. 把函数
 的图象向右平移
的图象向右平移 个单位,所得图象对应的函数为奇函数
个单位,所得图象对应的函数为奇函数 -
科目: 来源: 题型:
查看答案和解析>>【题目】在某次测试中,卷面满分为100分,考生得分为整数,规定60分及以上为及格.某调研课题小组为了调查午休对考生复习效果的影响,对午休和不午休的考生进行了测试成绩的统计,数据如下表:

(1)根据上述表格完成下列列联表:

(2)判断“能否在犯错误的概率不超过0.010的前提下认为成绩及格与午休有关”?
(参考公式:
 ,其中
,其中 .)
.)
0.010
0.05
0.010
0.001

2.706
3.841
6.635
10.828
-
科目: 来源: 题型:
查看答案和解析>>【题目】对某种书籍的成本费
 (元)与印刷册数
(元)与印刷册数 (千册)的数据作了初步处理,得到下面的散点图及一些统计量的值.
(千册)的数据作了初步处理,得到下面的散点图及一些统计量的值.

表中
 .
.为了预测印刷20千册时每册的成本费,建立了两个回归模型:
 .
.(1)根据散点图,拟认为选择哪个模型预测更可靠?(只选出模型即可)
(2)根据所给数据和(1)中的模型选择,求
 关于
关于 的回归方程,并预测印刷20千册时每册的成本费.
的回归方程,并预测印刷20千册时每册的成本费.附:对于一组数据
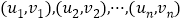 ,其回归方程
,其回归方程 中斜率和截距的最小二乘估计公式分别为:
中斜率和截距的最小二乘估计公式分别为: ,
, .
.
相关试题

