【题目】已知二次函数f(x)的二次项系数为a,且f(x)>﹣x的解集为{x|1<x<2},方程f(x)+2a=0有两相等实根,求f(x)的解析式.
参考答案:
【答案】解:设f(x)=ax2+bx+c,由f(x)>﹣x,可得ax2+(b+1)x+c>0,∵f(x)>﹣x的解集为{x|1<x<2},
∴ 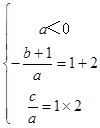 ,解得
,解得  ,
,
∴f(x)=ax2﹣(3a+1)x+2a.
∵f(x)+2a=0,即ax2﹣(3a+1)x+4a=0有两相等实根,
∴△=(3a+1)2﹣16a2=0,解得a=1舍去或 ![]() .④
.④
由①②③④得: ![]() ,
, ![]() ,
, ![]() .
.
∴ ![]()
【解析】设f(x)=ax2+bx+c,由f(x)>﹣x,可得ax2+(b+1)x+c>0,由f(x)>﹣x的解集为{x|1<x<2},列出不等式组,求解即可得a,b,c的关系式,再由f(x)+2a=0求出a的值,结合a,b,c的关系式即可得答案.
【考点精析】掌握函数的定义域及其求法是解答本题的根本,需要知道求函数的定义域时,一般遵循以下原则:①![]() 是整式时,定义域是全体实数;②
是整式时,定义域是全体实数;②![]() 是分式函数时,定义域是使分母不为零的一切实数;③
是分式函数时,定义域是使分母不为零的一切实数;③![]() 是偶次根式时,定义域是使被开方式为非负值时的实数的集合;④对数函数的真数大于零,当对数或指数函数的底数中含变量时,底数须大于零且不等于1,零(负)指数幂的底数不能为零.
是偶次根式时,定义域是使被开方式为非负值时的实数的集合;④对数函数的真数大于零,当对数或指数函数的底数中含变量时,底数须大于零且不等于1,零(负)指数幂的底数不能为零.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某市为了制定合理的节电方案,供电局对居民用电进行了调查,通过抽样,获得了某年200户居民每户的月均用电量(单位:度),将数据按照
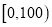 ,
, 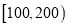 ,
, 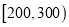 ,
, 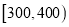 ,
, 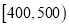 ,
, 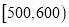 ,
, 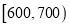 ,
, 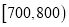 ,
, 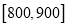 分成9组,制成了如图所示的频率分布直方图.
分成9组,制成了如图所示的频率分布直方图.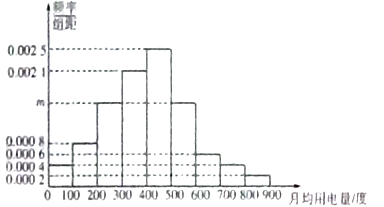
(Ⅰ)求直方图中
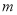 的值并估计居民月均用电量的中位数;
的值并估计居民月均用电量的中位数;(Ⅱ)现从第8组和第9组的居民中任选取2户居民进行访问,则两组中各有一户被选中的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=|2x﹣a|,g(x)=x+1.
(1)若a=1,求不等式f(x)≤1的解集;
(2)对任意的x∈R,f(x)+|g(x)|≥a2+2a(a>0)恒成立,求实数a的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四棱锥
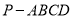 中,底面
中,底面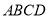 是正方形,
是正方形, 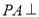 底面
底面 ,
,  ,
, 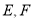 分别是
分别是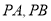 的中点.
的中点.(1)在图中画出过点
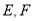 的平面
的平面 ,使得
,使得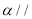 平面
平面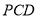 (须说明画法,并给予证明);
(须说明画法,并给予证明);(2)若过点
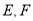 的平面
的平面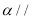 平面
平面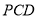 且截四棱锥
且截四棱锥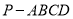 所得截面的面积为
所得截面的面积为 ,求四棱锥
,求四棱锥 的体积.
的体积.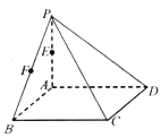
-
科目: 来源: 题型:
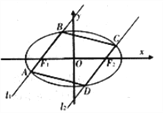
查看答案和解析>>【题目】如图,过椭圆
 :
: 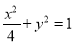 的左右焦点
的左右焦点 分别作直线
分别作直线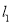 ,
, 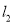 交椭圆于
交椭圆于 与
与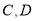 ,且
,且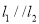 .
.
(1)求证:当直线
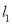 的斜率
的斜率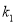 与直线
与直线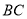 的斜率
的斜率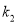 都存在时,
都存在时, 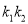 为定值;
为定值;(2)求四边形
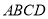 面积的最大值.
面积的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知正四棱柱的底面边长为
 ,高为
,高为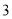 ,现从该正四棱柱的
,现从该正四棱柱的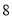 个顶点中任取
个顶点中任取 个点.设随机变量
个点.设随机变量 的值为以取出的
的值为以取出的 个点为顶点的三角形的面积.
个点为顶点的三角形的面积.(1)求概率
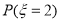 ;
;(2)求
 的分布列,并求其数学期望
的分布列,并求其数学期望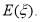
-
科目: 来源: 题型:
查看答案和解析>>【题目】设函数
 ,其中
,其中 ,且
,且 .
.(1)求
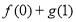 值;
值;(2)若
 ,
, 为自然对数的底数,求证:当
为自然对数的底数,求证:当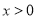 时,
时,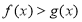 ;
;(3)若函数
 为
为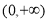 上的单调函数,求实数
上的单调函数,求实数 的取值范围.
的取值范围.
相关试题

