【题目】设函数![]() ,其中
,其中![]() ,且
,且![]() .
.
(1)求![]() 值;
值;
(2)若![]() ,
,![]() 为自然对数的底数,求证:当
为自然对数的底数,求证:当![]() 时,
时,![]() ;
;
(3)若函数![]() 为
为![]() 上的单调函数,求实数
上的单调函数,求实数![]() 的取值范围.
的取值范围.
参考答案:
【答案】见解析
【解析】(1)依题意![]() .……………2分
.……………2分
(2)记![]() ,则
,则![]() ,
,
设![]() ,则当
,则当![]() 时
时![]() ,因此函数
,因此函数![]() 在
在![]() 上是单调增函数,且
上是单调增函数,且![]() ,
,
所以由零点存在定理知,![]() 在
在![]() 上存在唯一的零点
上存在唯一的零点![]() ,……………5分
,……………5分
令![]() 得
得![]() ,
,
列表:
|
|
|
|
|
|
|
|
| ↘ | 极小值 | ↗ |
所以![]() ,故
,故![]() ……………8分
……………8分
(3)依题意,![]() ,记
,记![]() .
.
![]() 当
当![]() 时,
时,![]()
①若![]() 为
为![]() 上的单调增函数,则
上的单调增函数,则![]() ,即
,即![]() 在
在![]() 上恒成立
上恒成立
因为![]() 为
为![]() 上的单调增函数
上的单调增函数
所以![]() ,从而
,从而![]() ,舍去. ……………10分
,舍去. ……………10分
②若![]() 为
为![]() 上的单调减函数,则
上的单调减函数,则![]() ,即
,即![]() 在
在![]() 上恒成立
上恒成立
因为![]() ,
,
所以![]() 在
在![]() 上不恒成立,舍去. ……………12分
上不恒成立,舍去. ……………12分
![]() 当
当![]() 时,
时,![]()
①若![]() 为
为![]() 上的单调增函数,则
上的单调增函数,则![]() ,即
,即![]() 在
在![]() 上恒成立
上恒成立
由![]() 得
得![]() ,
,
列表:
|
|
|
|
| + | 0 | - |
| ↗ | 极大值 | ↘ |
所以![]()
所以![]() ,即
,即![]() ,故
,故![]() ……………14分
……………14分
②若![]() 为
为![]() 上的单调减函数,则
上的单调减函数,则![]() ,即
,即![]() 在
在![]() 上恒成立
上恒成立
由![]() ①知,当
①知,当![]() 时,
时,![]() ;当
;当![]() ,
,![]()
所以![]() ,不成立,舍去
,不成立,舍去
综上,![]() ……………16分
……………16分
备注:由函数图象能得出若单调必递增(因为图象交点左侧y小于0,右侧y大于0),可减少对![]() 的讨论.
的讨论.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数f(x)的二次项系数为a,且f(x)>﹣x的解集为{x|1<x<2},方程f(x)+2a=0有两相等实根,求f(x)的解析式.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,过椭圆
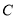 :
: 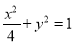 的左右焦点
的左右焦点 分别作直线
分别作直线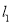 ,
, 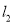 交椭圆于
交椭圆于 与
与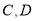 ,且
,且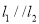 .
.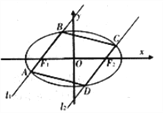
(1)求证:当直线
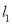 的斜率
的斜率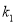 与直线
与直线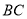 的斜率
的斜率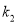 都存在时,
都存在时, 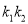 为定值;
为定值;(2)求四边形
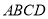 面积的最大值.
面积的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知正四棱柱的底面边长为
 ,高为
,高为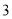 ,现从该正四棱柱的
,现从该正四棱柱的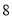 个顶点中任取
个顶点中任取 个点.设随机变量
个点.设随机变量 的值为以取出的
的值为以取出的 个点为顶点的三角形的面积.
个点为顶点的三角形的面积.(1)求概率
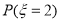 ;
;(2)求
 的分布列,并求其数学期望
的分布列,并求其数学期望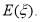
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆C:
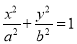 (a>b>0)的离心率为
(a>b>0)的离心率为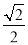 ,直线y=x+2过椭圆C的左焦点F1.
,直线y=x+2过椭圆C的左焦点F1.(1)求椭圆C的标准方程;
(2)设过点A(0,﹣1)的直线l与椭圆交于不同两点M、N,当△MON的面积为
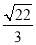 时,求直线l的方程.
时,求直线l的方程. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示的钢板的边界
 是抛物线的一部分,且
是抛物线的一部分,且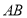 垂直于抛物线对称轴,现欲从钢板上截取一块以
垂直于抛物线对称轴,现欲从钢板上截取一块以 为下底边的等腰梯形钢板
为下底边的等腰梯形钢板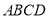 ,其中
,其中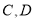 均在抛物线弧上.设
均在抛物线弧上.设 (米),且
(米),且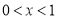 .
.(1)当
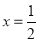 时,求等腰梯形钢板的面积;
时,求等腰梯形钢板的面积;(2)当
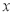 为何值时,等腰梯形钢板的面积最大?并求出最大值.
为何值时,等腰梯形钢板的面积最大?并求出最大值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=x3+
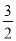 x2+mx在x=1处有极小值,
x2+mx在x=1处有极小值,g(x)=f(x)﹣
 x3﹣
x3﹣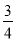 x2+x﹣alnx.
x2+x﹣alnx.(1)求函数f(x)的单调区间;
(2)是否存在实数a,对任意的x1、x2∈(0,+∞),且x1≠x2,有
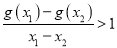 恒成立?若存在,求出a的取值范围;若不存在,说明理由.
恒成立?若存在,求出a的取值范围;若不存在,说明理由.
相关试题

