【题目】某校从高一年级学生中随机抽取40名学生,将他们的期中考试数学成绩(满分100分,成绩均为不低于40分的整数)分成六段:[40,50),[50,60),…,[90,100]后得到如图所示的频率分布直方图,其中前三段的频率成等比数列.

(Ⅰ)求图中实数a,b的值;
(Ⅱ)若该校高一年级共有学生640人,试估计该校高一年级期中考试数学成绩不低于80分的人数;
(Ⅲ)若从样本中数学成绩在[40,50)与[90,100]两个分数段内的学生中随机选取两名学生,求这两名学生的数学成绩之差的绝对值大于10的概率.
参考答案:
【答案】(Ⅰ) b=0.010,a=0.030(Ⅱ)224(Ⅲ) ![]() .
.
【解析】试题分析:(Ⅰ)因为前三段的频率成等比数列,所以由等比数列性质及频率分布直方图的性质,可列出关于![]() 方程组,从而能求出
方程组,从而能求出![]() ;(Ⅱ) 利用频率分布直方图能求出成绩不低于
;(Ⅱ) 利用频率分布直方图能求出成绩不低于![]() 分的频率,频率与总人数的积就是成绩不低于
分的频率,频率与总人数的积就是成绩不低于![]() 分的人数;(Ⅲ) 样本中成绩在
分的人数;(Ⅲ) 样本中成绩在![]() 内的人数为
内的人数为![]() ,成绩在
,成绩在![]() 内的人数为
内的人数为![]() 从
从![]() 人中任选
人中任选![]() 人共有
人共有![]() 种等可能性选法,两人成绩差的绝对值大于
种等可能性选法,两人成绩差的绝对值大于![]() 的选法有
的选法有![]() 种,由古典概型概率公式可得结果.
种,由古典概型概率公式可得结果.
试题解析:(Ⅰ)由直方图及题意得(10b)2=0.05×0.20.∴b=0.010,
∴a=0.1-0.005-0.010-0.020-0.025-0.010=0.030.
(Ⅱ)成绩不低于80分的人数估计为640×(0.025+0.010)×10=224.
(Ⅲ)两个分数段的学生分别为2,4;从6人中任选2人共有15种等可能性选法,
两人成绩差的绝对值大于10的选法有8种,
故所求事件的概率为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=
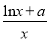 (a∈R).
(a∈R).(Ⅰ)求f(x)的单调区间与极值;
(Ⅱ)若函数f(x)的图象与函数g(x)=1的图象在区间(0,e2]上有两个公共点,求实数a的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在直角坐标系xOy中,曲线M的参数方程为
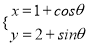 (θ为参数),若以直角坐标系的原点O为极点,x轴的正半轴为极轴建立极坐标系,曲线N的极坐标方程为ρsin(θ+
(θ为参数),若以直角坐标系的原点O为极点,x轴的正半轴为极轴建立极坐标系,曲线N的极坐标方程为ρsin(θ+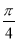 )=
)=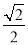 t(其中t为常数).
t(其中t为常数).(Ⅰ)若曲线N与曲线M只有一个公共点,求t的值;
(Ⅱ)当t=-1时,求曲线M上的点与曲线N上的点的最小距离.
-
科目: 来源: 题型:
查看答案和解析>>【题目】设函数f(x)=|x-1|+|x-a|,a∈R.
(Ⅰ)当a=4时,求不等式f(x)≥7的解集;
(Ⅱ)若f(x)≥5对x∈R恒成立,求a的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在三棱柱ABC-A1B1C1中,CC1⊥平面ABC,M是CC1中点.

(Ⅰ)求证:平面AB1M⊥平面A1ABB1;
(Ⅱ)过点C作一截面与平面AB1M平行,并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆C:
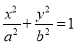 (a>b>0)经过点(
(a>b>0)经过点(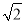 ,1),以原点为圆心、椭圆短半轴长为半径的圆经过椭圆的焦点.
,1),以原点为圆心、椭圆短半轴长为半径的圆经过椭圆的焦点.(Ⅰ)求椭圆C的方程;
(Ⅱ)设过点(-1,0)的直线l与椭圆C相交于A,B两点,试问在x轴上是否存在一个定点M,使得
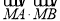 恒为定值?若存在,求出该定值及点M的坐标;若不存在,请说明理由.
恒为定值?若存在,求出该定值及点M的坐标;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】函数f(x)=a
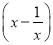 -2ln x(a∈R).
-2ln x(a∈R).(Ⅰ)当a=2时,求曲线f(x)在x=2处的切线方程;
(Ⅱ)若a>
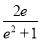 ,且m,n分别为f(x)的极大值和极小值,S=m-n,求证:S<
,且m,n分别为f(x)的极大值和极小值,S=m-n,求证:S<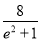 .
.
相关试题

