【题目】函数f(x)=a![]() -2ln x(a∈R).
-2ln x(a∈R).
(Ⅰ)当a=2时,求曲线f(x)在x=2处的切线方程;
(Ⅱ)若a>![]() ,且m,n分别为f(x)的极大值和极小值,S=m-n,求证:S<
,且m,n分别为f(x)的极大值和极小值,S=m-n,求证:S<![]() .
.
参考答案:
【答案】(Ⅰ)3x-2y-4ln 2=0(Ⅱ)见解析
【解析】试题分析:(Ⅰ) 求出导数,计算![]() 可得到切线斜率,求出
可得到切线斜率,求出![]() 可得切点坐标,利用点斜式即可求出切线方程;(Ⅱ) 设
可得切点坐标,利用点斜式即可求出切线方程;(Ⅱ) 设![]() 的两根为
的两根为![]() ,所以
,所以![]() ,求出
,求出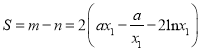 ,将
,将![]() 的值代入
的值代入![]() 的解析式,化简,构造新函数
的解析式,化简,构造新函数![]() ,求导数,利用导数研究函数的单调性,应用单调性求最值,即可证明结论.
,求导数,利用导数研究函数的单调性,应用单调性求最值,即可证明结论.
试题解析:(Ⅰ) f′(x)=a+![]() -
-![]() ,若a=2,则f′(2)=2+
,若a=2,则f′(2)=2+![]() -
-![]() =
=![]() ,f(2)=4-1-2ln 2=3-2ln 2,则曲线f(x)在x=2处的切线方程为y-(3-2ln 2)=
,f(2)=4-1-2ln 2=3-2ln 2,则曲线f(x)在x=2处的切线方程为y-(3-2ln 2)=![]() (x-2),化简得3x-2y-4ln 2=0.
(x-2),化简得3x-2y-4ln 2=0.
(Ⅱ)f′(x)=![]() ,令f′(x)=0,得ax2-2x+a=0,
,令f′(x)=0,得ax2-2x+a=0,
则Δ>0且![]() <a,得
<a,得![]() <a<1,此时设f′(x)=0的两根为x1,x2(x1<x2),
<a<1,此时设f′(x)=0的两根为x1,x2(x1<x2),
所以m=f(x1),n=f(x2).
因为x1x2=1,所以x1<1<x2,由![]() <a<1,
<a<1,
所以S=m-n=ax1-![]() -2ln x1-(ax2-
-2ln x1-(ax2-![]() -2ln x2)
-2ln x2)
=ax1-![]() -2ln x1-(
-2ln x1-(![]() -ax1+2ln x1)
-ax1+2ln x1)
=2(ax1-![]() -2ln x1).
-2ln x1).
由a![]() -2x1+a=0得a=
-2x1+a=0得a=![]() ,
,
代入上式得S=4(![]() -lnx1)
-lnx1)
=4(![]() -
-![]() ln
ln![]() ).
).
令h(x)=ax2-2x+a,则h![]() =
=![]() -
-![]() +a
+a
=a·![]() -
-![]() >
>![]() ·
·![]() -
-![]() =
=![]() -
-![]() =0,
=0,
x=![]()
![]() 是抛物线h(x)的对称轴.
是抛物线h(x)的对称轴.
∴![]() <x1<1.
<x1<1.
令![]() =t,所以
=t,所以![]() <t<1,g(x)=
<t<1,g(x)=![]() -
-![]() ln x,则S=4g(t),
ln x,则S=4g(t),
g'(x)=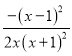 <0,所以g(x)在
<0,所以g(x)在![]() ≤x≤1上为减函数,
≤x≤1上为减函数,
从而g(1)<g(t)<g(![]() ),即0<g(t)<
),即0<g(t)< ![]() ,所以S<
,所以S<![]() .
.
【方法点晴】本题主要考查利用导数求曲线切线方程以及利用导数研究函数的单调性与极值,属于难题.求曲线切线方程的一般步骤是:(1)求出![]() 在
在![]() 处的导数,即
处的导数,即![]() 在点
在点![]()
![]() 出的切线斜率(当曲线
出的切线斜率(当曲线![]() 在
在![]() 处的切线与
处的切线与![]() 轴平行时,在 处导数不存在,切线方程为
轴平行时,在 处导数不存在,切线方程为![]() );(2)由点斜式求得切线方程
);(2)由点斜式求得切线方程![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校从高一年级学生中随机抽取40名学生,将他们的期中考试数学成绩(满分100分,成绩均为不低于40分的整数)分成六段:[40,50),[50,60),…,[90,100]后得到如图所示的频率分布直方图,其中前三段的频率成等比数列.

(Ⅰ)求图中实数a,b的值;
(Ⅱ)若该校高一年级共有学生640人,试估计该校高一年级期中考试数学成绩不低于80分的人数;
(Ⅲ)若从样本中数学成绩在[40,50)与[90,100]两个分数段内的学生中随机选取两名学生,求这两名学生的数学成绩之差的绝对值大于10的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在三棱柱ABC-A1B1C1中,CC1⊥平面ABC,M是CC1中点.

(Ⅰ)求证:平面AB1M⊥平面A1ABB1;
(Ⅱ)过点C作一截面与平面AB1M平行,并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆C:
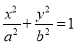 (a>b>0)经过点(
(a>b>0)经过点(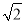 ,1),以原点为圆心、椭圆短半轴长为半径的圆经过椭圆的焦点.
,1),以原点为圆心、椭圆短半轴长为半径的圆经过椭圆的焦点.(Ⅰ)求椭圆C的方程;
(Ⅱ)设过点(-1,0)的直线l与椭圆C相交于A,B两点,试问在x轴上是否存在一个定点M,使得
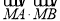 恒为定值?若存在,求出该定值及点M的坐标;若不存在,请说明理由.
恒为定值?若存在,求出该定值及点M的坐标;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】在直角坐标系中,以坐标原点为极点,x轴正半轴为极轴建立极坐标系,圆C的极坐标方程为ρ=4cosθ-2sinθ.
(Ⅰ)求C的参数方程;
(Ⅱ)若点A在圆C上,点B(3,0),求AB中点P到原点O的距离平方的最大值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=|3x-1|-2|x|+2.
(Ⅰ)解不等式:f(x)<10;
(Ⅱ)若对任意的实数x,f(x)-|x|≤a恒成立,求实数a的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在三棱锥PABC中,不能证明AP⊥BC的条件是( )

A. AP⊥PB,AP⊥PC
B. AP⊥PB,BC⊥PB
C. 平面BPC⊥平面APC,BC⊥PC
D. AP⊥平面PBC
相关试题

