【题目】已知函数![]() ,
, ![]()
(Ⅰ)当![]() 时,求函数
时,求函数![]() 的单调区间;
的单调区间;
(Ⅱ)若![]() 对任意
对任意![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
参考答案:
【答案】解:(Ⅰ)函数![]() 在
在![]() 上单调递减,在
上单调递减,在![]() ,
, ![]() 上单调递增. (Ⅱ)
上单调递增. (Ⅱ)![]()
【解析】试题分析:(Ⅰ)当![]() 时,
时, ![]() ,求导因式分解可得单调区间;
,求导因式分解可得单调区间;
(2)利用导数将不等式恒成立问题转化为对单调性的讨论,再利用单调性求解参数范围.
试题解析:(Ⅰ)当![]() 时,
时, ![]()
则![]() ,
,
![]()
此时:函数![]() 在
在![]() 上单调递减,在
上单调递减,在![]() ,
, ![]() 上单调递增.
上单调递增.
(Ⅱ)依题意有: ![]()
![]() ,
,
令![]() ,
,
得: ![]() ,
,
①当![]() 即
即![]() 时,
时,
函数![]() 在
在![]() 恒成立,
恒成立,
则![]() 在
在![]() 单调递增,
单调递增,
于是![]() ,
,
解得: ![]() ;
;
②当![]() 即
即![]() 时,
时,
函数![]() 在
在![]() 单调递减,在
单调递减,在![]() 单调递增,
单调递增,
于是![]() ,不合题意,
,不合题意,
此时: ![]() ;
;
综上所述:实数![]() 的取值范围是
的取值范围是![]()
点晴:本题主要考查函数单调性,不等式恒成立问题.要求单调性,求导比较导方程的根的大小,解不等式可得单调区间,要证明不等式恒成立问题可转化为构造新函数证明新函数单调,只需要证明其导函数大于等于0(或者恒小于等于0即可),要证明一个不等式,我们可以先根据题意构造新函数,求其值最值即可.
-
科目: 来源: 题型:
查看答案和解析>>【题目】以下是解决数学问题的思维过程的流程图:
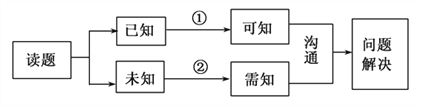
在此流程图中,①、②两条流程线与“推理与证明”中的思维方法匹配正确的是( )
A.
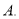 ①—分析法,②—反证法 B. ①—分析法,②—综合法
①—分析法,②—反证法 B. ①—分析法,②—综合法C. ①—综合法,②—反证法 D. ①—综合法,②—分析法
-
科目: 来源: 题型:
查看答案和解析>>【题目】给出下列命题:
①若(1-x)5=a0+a1x+a2x2+a3x3+a4x4+a5x5,则|a1|+|a2|+|a3|+|a4|+|a5|=32
②α,β,γ是三个不同的平面,则“γ⊥α,γ⊥β”是“α∥β”的充分条件
③已知sin
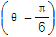 =
=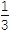 ,则cos
,则cos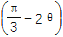 =
=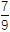 .其中正确命题的个数为( )
.其中正确命题的个数为( )A.0 B.1
C.2 D.3
-
科目: 来源: 题型:
查看答案和解析>>【题目】下面几种推理是合情推理的是
①由圆的性质类比出球的有关性质;②由直角三角形、等腰三角形、等边三角形的内角和是180°,归纳出所有三角形的内角和都是180°;③教室内有一把椅子坏了,则该教室内的所有椅子都坏了;④三角形内角和是180°,四边形内角和是360°,五边形内角和是540°,由此得出凸多边形的内角和是(n-2)·180°___________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知等差数列{an}的前3项和为6,前8项和为-4.
(1)求数列{an}的通项公式;
(2)设bn=(4-an)qn-1 (q≠0,n∈N*),求数列{bn}的前n项和Sn.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在某地区某高传染性病毒流行期间,为了建立指标显示疫情已受控制,以便向该地区居众显示可以过正常生活,有公共卫生专家建议的指标是“连续7天每天新增感染人数不超过5人”,根据连续7天的新增病例数计算,下列各选项中,一定符合上述指标的是( )
①平均数
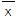 ≤3;②标准差S≤2;③平均数
≤3;②标准差S≤2;③平均数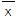 ≤3且标准差S≤2;④平均数
≤3且标准差S≤2;④平均数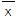 ≤3且极差小于或等于2;⑤众数等于1且极差小于或等于1.
≤3且极差小于或等于2;⑤众数等于1且极差小于或等于1.A.①② B.③④
C.③④⑤ D.④⑤
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数f(x)的最小值为1,且f(0)=f(2)=3.
(1)求f(x)的解析式;
(2)若f(x)在区间[2a,a+1]上不单调,求实数a的取值范围;
(3)在区间[-1,1]上,y=f(x)的图象恒在y=2x+2m+1的图象上方,试确定实数m的范围.
相关试题

