【题目】判断函数f(x)= ![]() 在(﹣1,+∞)上的单调性,并证明.
在(﹣1,+∞)上的单调性,并证明.
参考答案:
【答案】证明:设﹣1<x1<x2 , 则f(x1)﹣f(x2)= ![]() ﹣
﹣ ![]() =
= ![]()
= ![]()
∵﹣1<x1<x2 ,
∴x1﹣x2<0,x1+1>0,x2+1>0.
∴当a>0时,f(x1)﹣f(x2)<0,即f(x1)<f(x2),
∴函数y=f(x)在(﹣1,+∞)上单调递增.
同理当a<0时,f(x1)﹣f(x2)>0,即f( x1)>f(x2),
∴函数y=f(x)在(﹣1,+∞)上单调递减
【解析】设﹣1<x1<x2 , 求出f(x1)﹣f(x2)的表达式,通过讨论a的范围,从而得出函数的单调区间.
【考点精析】利用函数单调性的判断方法对题目进行判断即可得到答案,需要熟知单调性的判定法:①设x1,x2是所研究区间内任两个自变量,且x1<x2;②判定f(x1)与f(x2)的大小;③作差比较或作商比较.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知实数
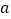 ,
,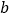 满足
满足 ,实数
,实数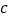 ,
,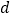 满足
满足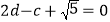 ,则
,则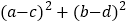 的最小值为__________.
的最小值为__________. -
科目: 来源: 题型:
查看答案和解析>>【题目】为了得到函数y=cos(2x+
 ),x∈R的图象,只需把函数y=cos2x的图象( )
),x∈R的图象,只需把函数y=cos2x的图象( )
A.向左平行移动 个单位长度
个单位长度
B.向左平行移动 个单位长度
个单位长度
C.向右平行移动 个单位长度
个单位长度
D.向右平行移动 个单位长度
个单位长度 -
科目: 来源: 题型:
查看答案和解析>>【题目】某重点高中拟把学校打造成新型示范高中,为此制定了学生“七不准”,“一日三省十问”等新的规章制度.新规章制度实施一段时间后,学校就新规章制度随机抽取部分学生进行问卷调查,调查卷共有10个问题,每个问题10分,调查结束后,按分数分成5组:
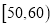 ,
, 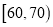 ,
, 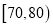 ,
, 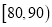 ,
,  ,并作出频率分布直方图与样本分数的茎叶图(图中仅列出了得分在
,并作出频率分布直方图与样本分数的茎叶图(图中仅列出了得分在 ,
, 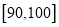 的数据).
的数据).(1)求样本容量
 和频率分布直方图中的
和频率分布直方图中的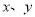 的值;
的值;(2)在选取的样本中,从分数在70分以下的学生中随机抽取2名学生进行座谈会,求所抽取的2名学生中恰有一人得分在
 内的概率.
内的概率.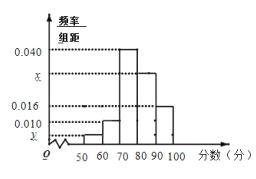

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<
 )的一段图象如下所示.
)的一段图象如下所示. 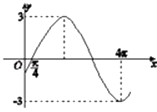
(1)求f(x)的解析式;
(2)求f(x)的单调减区间,并指出f(x)的最大值及取到最大值时x的集合. -
科目: 来源: 题型:
查看答案和解析>>【题目】某公司为了解广告投入对销售收益的影响,在若干地区各投入
 万元广告费用,并将各地的销售收益绘制成频率分布直方图(如图所示).由于工作人员操作失误,横轴的数据丢失,但可以确定横轴是从
万元广告费用,并将各地的销售收益绘制成频率分布直方图(如图所示).由于工作人员操作失误,横轴的数据丢失,但可以确定横轴是从 开始计数的. [附:回归直线的斜率和截距的最小二乘估计公式分别为.]
开始计数的. [附:回归直线的斜率和截距的最小二乘估计公式分别为.](1)根据频率分布直方图计算图中各小长方形的宽度;
(2)试估计该公司投入
 万元广告费用之后,对应销售收益的平均值(以各组的区间中点值代表该组的取值);
万元广告费用之后,对应销售收益的平均值(以各组的区间中点值代表该组的取值);(3)该公司按照类似的研究方法,测得另外一些数据,并整理得到下表:
广告投入
 (单位:万元)
(单位:万元)1
2
3
4
5
销售收益
 (单位:万元)
(单位:万元)2
3
2
7
由表中的数据显示,
 与
与 之间存在着线性相关关系,请将(2)的结果填入空白栏,并求出
之间存在着线性相关关系,请将(2)的结果填入空白栏,并求出 关于
关于 的回归直线方程.
的回归直线方程.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:
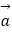 、
、 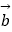 、
、 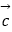 是同一平面上的三个向量,其中
是同一平面上的三个向量,其中 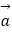 =(1,2).
=(1,2).
(1)若|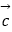 |=2
|=2 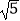 ,且
,且 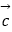 ∥
∥ 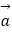 ,求
,求 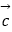 的坐标.
的坐标.
(2)若|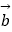 |=
|= 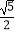 ,且
,且 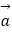 +2
+2 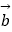 与2
与2 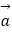 ﹣
﹣ 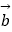 垂直,求
垂直,求 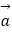 与
与 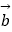 的夹角θ
的夹角θ
相关试题

