【题目】已知直四棱柱![]() 的底面ABCD是菱形,
的底面ABCD是菱形,![]() ,E是
,E是![]() 上任意一点.
上任意一点.
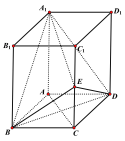
(1)求证:平面![]() 平面
平面![]() ;
;
(2)设![]() ,当E为
,当E为![]() 的中点时,求点E到平面
的中点时,求点E到平面![]() 的距离.
的距离.
参考答案:
【答案】(1)详见解析;(2)![]() .
.
【解析】
(1)由题,![]() ,又ABCD是菱形,那么
,又ABCD是菱形,那么![]() ,可知
,可知![]() 平面
平面![]() ,
,![]() 平面BDE,即得证;(2)由等体积法
平面BDE,即得证;(2)由等体积法![]() ,计算即得。
,计算即得。
解:(1)证明:∵四棱柱![]() 是直四棱柱,
是直四棱柱,
∴![]() 底面ABCD,而
底面ABCD,而![]() 底面ABCD,∴
底面ABCD,∴![]() .
.
又ABCD是菱形,有![]() ,∵
,∵![]() ,故
,故![]() 平面
平面![]()
又![]() 平面BDE,∴平面
平面BDE,∴平面![]() 平面
平面![]() .
.
(2)法一:设AC与BD的交点为O,连OE,![]() ,由(1)知点E到平面
,由(1)知点E到平面![]() 的距离即点E到直线
的距离即点E到直线![]() 的距离.又在三角形
的距离.又在三角形![]() 中,
中,![]() ,
,![]() ,得OE边上的高为
,得OE边上的高为![]() ,故E到直线
,故E到直线![]() 的距离
的距离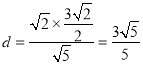 .
.
法二:由![]() ,而
,而![]() ,
,![]() ,
,
故![]() .
.
[Failed to download image : http://192.168.0.10:8086/QBM/2020/3/7/2414489840492544/2415946282483712/EXPLANATION/6b6d144eb17043c7bd8f25c3951e7b32.png]
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
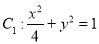 ,椭圆
,椭圆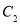 以
以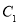 的长轴为短轴,且两个椭圆的离心率相同,设O为坐标原点,点A、B分别在椭圆
的长轴为短轴,且两个椭圆的离心率相同,设O为坐标原点,点A、B分别在椭圆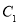 、
、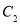 上,若
上,若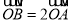 ,则直线AB的斜率k为( ).
,则直线AB的斜率k为( ).A.1B.-1C.
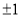 D.
D.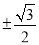
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知四棱锥
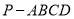 中,底面ABCD是梯形,且
中,底面ABCD是梯形,且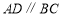 ,
, ,
,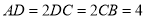 ,
,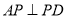 ,
,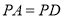 ,
, ,AD的中点为E,则四棱锥
,AD的中点为E,则四棱锥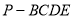 外接球的表面积为________.
外接球的表面积为________. -
科目: 来源: 题型:
查看答案和解析>>【题目】在新高考改革中,打破了文理分科的“
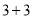 ”模式,不少省份采用了“
”模式,不少省份采用了“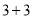 ”,“
”,“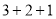 ”,“
”,“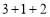 ”等模式.其中“
”等模式.其中“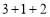 ”模式的操作又更受欢迎,即语数外三门为必考科目,然后在物理和历史中选考一门,最后从剩余的四门中选考两门.某校为了了解学生的选科情况,从高二年级的2000名学生(其中男生1100人,女生900人)中,采用分层抽样的方法从中抽取n名学生进行调查.
”模式的操作又更受欢迎,即语数外三门为必考科目,然后在物理和历史中选考一门,最后从剩余的四门中选考两门.某校为了了解学生的选科情况,从高二年级的2000名学生(其中男生1100人,女生900人)中,采用分层抽样的方法从中抽取n名学生进行调查.(1)已知抽取的n名学生中含男生110人,求n的值及抽取到的女生人数;
(2)在(1)的情况下对抽取到的n名同学“选物理”和“选历史”进行问卷调查,得到下列2×2列联表.请将列联表补充完整,并判断是否有99%的把握认为选科目与性别有关?
选物理
选历史
合计
男生
90
女生
30
合计
(3)在(2)的条件下,从抽取的“选历史”的学生中按性别分层抽样再抽取5名,再从这5名学生中抽取2人了解选政治、地理、化学、生物的情况,求2人至少有1名男生的概率.
参考公式:
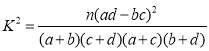 .
.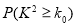
0.10
0.010
0.001
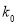
2.706
6.635
10.828
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
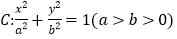 的离心率为
的离心率为 ,左、右焦点分别是
,左、右焦点分别是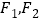 ,椭圆
,椭圆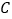 上短轴的一个端点与两个焦点构成的三角形的面积为
上短轴的一个端点与两个焦点构成的三角形的面积为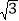 ;
;(1)求椭圆
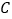 的方程;
的方程;(2)过
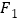 作垂直于
作垂直于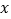 轴的直线
轴的直线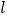 交椭圆
交椭圆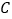 于
于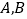 两点(点
两点(点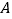 在第二象限),
在第二象限),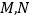 是椭圆上位于直线
是椭圆上位于直线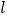 两侧的动点,若
两侧的动点,若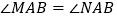 ,求证:直线
,求证:直线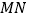 的斜率为定值.
的斜率为定值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
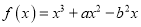 ,其中
,其中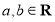 .
.(1)若曲线
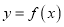 在点
在点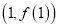 处的切线与直线
处的切线与直线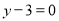 平行,求
平行,求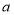 与
与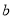 满足的关系;
满足的关系;(2)当
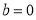 时,讨论
时,讨论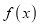 的单调性;
的单调性;(3)当
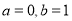 时,对任意的
时,对任意的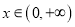 ,总有
,总有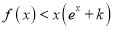 成立,求实数
成立,求实数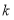 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】在直角坐标系
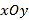 中,倾斜角为
中,倾斜角为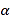 的直线
的直线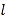 的参数方程为
的参数方程为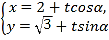 (
(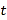 为参数).在以坐标原点为极点,
为参数).在以坐标原点为极点,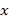 轴正半轴为极轴的极坐标系中,曲线
轴正半轴为极轴的极坐标系中,曲线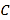 的极坐标方程为
的极坐标方程为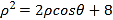 .
.(1)求直线
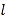 的普通方程与曲线
的普通方程与曲线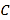 的直角坐标方程;
的直角坐标方程;(2)若直线
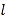 与曲线
与曲线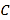 交于
交于 ,
, 两点,且
两点,且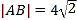 ,求直线
,求直线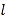 的倾斜角.
的倾斜角.
相关试题

