【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,左、右焦点分别是
,左、右焦点分别是![]() ,椭圆
,椭圆![]() 上短轴的一个端点与两个焦点构成的三角形的面积为
上短轴的一个端点与两个焦点构成的三角形的面积为![]() ;
;
(1)求椭圆![]() 的方程;
的方程;
(2)过![]() 作垂直于
作垂直于![]() 轴的直线
轴的直线![]() 交椭圆
交椭圆![]() 于
于![]() 两点(点
两点(点![]() 在第二象限),
在第二象限),![]() 是椭圆上位于直线
是椭圆上位于直线![]() 两侧的动点,若
两侧的动点,若![]() ,求证:直线
,求证:直线![]() 的斜率为定值.
的斜率为定值.
参考答案:
【答案】(1)![]() ;(2)证明见解析.
;(2)证明见解析.
【解析】
(1)根据离心率和三角形面积可构造关于![]() 的方程,解方程可求得
的方程,解方程可求得![]() ,进而得到椭圆方程;(2)假设直线方程,代入椭圆方程,利用韦达定理得到
,进而得到椭圆方程;(2)假设直线方程,代入椭圆方程,利用韦达定理得到![]() 和
和![]() ;根据
;根据![]() 知
知![]() ,从而可利用韦达定理形式表示出等式,化简可得
,从而可利用韦达定理形式表示出等式,化简可得![]() ;当
;当![]() 时,可知过
时,可知过![]() 点,不符合题意;所以可知
点,不符合题意;所以可知![]() .
.
(1)由题意可得:![]() 且
且![]()
又![]() 得:
得:![]() ,
,![]() ,
,![]()
![]() 椭圆
椭圆![]() 的方程为
的方程为![]()
(2)证明:由(1)可得:直线![]() :
:![]() ,
,![]()
设直线![]() 的方程为
的方程为![]() ,代入椭圆方程
,代入椭圆方程
消![]() 可得
可得![]()
设![]() ,
,![]() ,则
,则![]()
则![]() ,
,![]()
![]()
![]()
![]()
即![]()
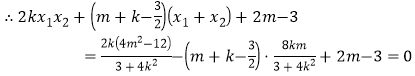 化简可得
化简可得![]()
![]() 或
或![]()
当![]() 时,直线
时,直线![]() 的方程为
的方程为![]()
则直线![]() 经过点
经过点![]() ,不满足题意
,不满足题意
![]()
即直线![]() 的斜率为定值
的斜率为定值![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系
 中,O为坐标原点,以O为圆心的圆与直线
中,O为坐标原点,以O为圆心的圆与直线 相切.
相切.(1)求圆O的方程.
(2)直线
 与圆O交于A,B两点,在圆O上是否存在一点M,使得四边形
与圆O交于A,B两点,在圆O上是否存在一点M,使得四边形 为菱形?若存在,求出此时直线l的斜率;若不存在,说明理由.
为菱形?若存在,求出此时直线l的斜率;若不存在,说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】某校设计了一个实验考察方案:考生从6道备选题中一次性随机抽取3题,按照题目要求独立完成全部实验操作,规定:至少正确完成其中2道题的便可通过.已知6道备选题中考生甲有4道题能正确完成,2道题不能完成,考生乙每题正确完成的概率都是
 ,且每题正确完成与否互不影响.
,且每题正确完成与否互不影响.(1)求甲、乙两考生正确完成题数的分布列,并计算其数学期望;
(2)请分析比较甲、乙两考生的实验操作能力.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线
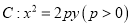 过点
过点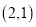 ,直线
,直线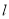 过点
过点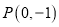 与抛物线
与抛物线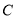 交于
交于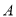 ,
,  两点.点
两点.点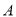 关于
关于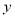 轴的对称点为
轴的对称点为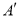 ,连接
,连接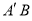 .
.
(1)求抛物线线
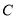 的标准方程;
的标准方程;(2)问直线
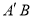 是否过定点?若是,求出定点坐标;若不是,请说明理由.
是否过定点?若是,求出定点坐标;若不是,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】某市场研究人员为了了解产业园引进的甲公司前期的经营状况,对该公司2019年连续六个月(5-10)月)的利润进行了统计,并根据得到的数据绘制了相应的折线图,如图所示.
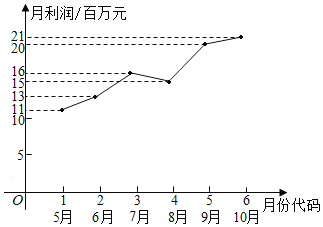
(1)由折线图可以看出,可用线性回归模型拟合月利润
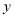 (单位:百万元)与月份代码
(单位:百万元)与月份代码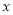 之间的关系,求
之间的关系,求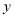 关于
关于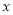 的线性回归方程,并据此预测该公司2020年5月份的利润;
的线性回归方程,并据此预测该公司2020年5月份的利润;(2)甲公司新研制了一款产品,需要采购一批新型材料,现有
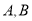 两种型号的新型材料可供选择,按规定每种新型材料最多可使用4个月,但新材料的不稳定性会导致材料损坏的年限不同,现对
两种型号的新型材料可供选择,按规定每种新型材料最多可使用4个月,但新材料的不稳定性会导致材料损坏的年限不同,现对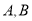 两种型号的新型材料对应的产品各100件进行科学模拟测试,得到两种新型材料使用寿命的频数统计表(表).若从产品使用寿命的角度考虑,甲公司的负责人选择采购哪款新型材料更好?
两种型号的新型材料对应的产品各100件进行科学模拟测试,得到两种新型材料使用寿命的频数统计表(表).若从产品使用寿命的角度考虑,甲公司的负责人选择采购哪款新型材料更好?使用寿命
1个月
2个月
3个月
4个月
总计
材料类型
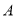
20
35
35
10
100
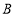
10
30
40
20
100
参考数据:
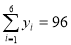 ,
,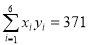 .
.参考公式:回归直线方程
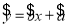 ,其中
,其中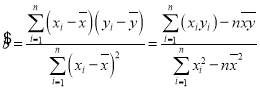 ,
,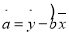 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 ,
,  .
.(Ⅰ)若函数
 为定义域上的单调函数,求实数
为定义域上的单调函数,求实数 的取值范围;
的取值范围;(Ⅱ)若函数
 存在两个极值点
存在两个极值点 ,
,  ,且
,且 ,证明:
,证明:  .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在梯形
 中,
中,  ,
, 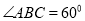 .
. 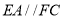 ,且
,且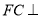 平面
平面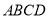 ,
, 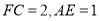 ,点
,点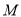 为
为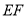 上任意一点.
上任意一点.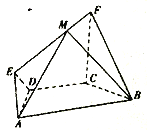
(1)求证:
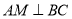 ;
;(2)点
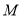 在线段
在线段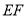 上运动(包括两端点),若平面
上运动(包括两端点),若平面 与平面
与平面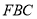 所成的锐二面角为60°,试确定点
所成的锐二面角为60°,试确定点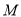 的位置.
的位置.
相关试题

