【题目】已知椭圆![]() ,椭圆
,椭圆![]() 以
以![]() 的长轴为短轴,且两个椭圆的离心率相同,设O为坐标原点,点A、B分别在椭圆
的长轴为短轴,且两个椭圆的离心率相同,设O为坐标原点,点A、B分别在椭圆![]() 、
、![]() 上,若
上,若![]() ,则直线AB的斜率k为( ).
,则直线AB的斜率k为( ).
A.1B.-1C.![]() D.
D.![]()
参考答案:
【答案】C
【解析】
先由已知求出椭圆![]() 的标准方程,设点A,B的坐标分别为
的标准方程,设点A,B的坐标分别为![]() ,由
,由![]() 可知O,A,B三点共线,由椭圆
可知O,A,B三点共线,由椭圆![]() ,
,![]() 的标准方程可知A,B两点不在y轴上,因此设AB的方程为
的标准方程可知A,B两点不在y轴上,因此设AB的方程为![]() ,将
,将![]() 分别与椭圆
分别与椭圆![]() ,
,![]() 的方程联立消去y,用k分别表示
的方程联立消去y,用k分别表示![]() ,由
,由![]() 可得含k的一元二次方程,解出k,即得。
可得含k的一元二次方程,解出k,即得。
由题得,椭圆![]() 的长轴为4,离心率
的长轴为4,离心率![]() ,
,![]() 椭圆
椭圆![]() 以
以![]() 的长轴为短轴,且两个椭圆的离心率相同,
的长轴为短轴,且两个椭圆的离心率相同,![]() 椭圆
椭圆![]() 的焦点在y轴上,
的焦点在y轴上,![]() ,
,![]() ,椭圆
,椭圆![]() 的方程为
的方程为![]() .设A,B坐标分别为
.设A,B坐标分别为![]() ,
,![]() ,
,![]() 三点共线,且点A,B不在y轴上,设AB的方程为
三点共线,且点A,B不在y轴上,设AB的方程为![]() ,代入
,代入![]() 得
得![]() ,
,![]() ,将
,将![]() 代入
代入![]() 得,
得,![]() ,
,![]() ,
,![]() ,
,![]() ,解得
,解得![]() .
.
故选:C
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
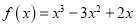 ,
,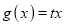 ,
,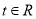 .
.(1)求函数
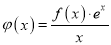 的单调增区间;
的单调增区间;(2)令
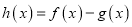 ,且函数
,且函数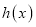 有三个彼此不相等的零点0,m,n,其中
有三个彼此不相等的零点0,m,n,其中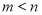 .
.①若
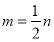 ,求函数
,求函数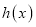 在
在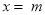 处的切线方程;
处的切线方程;②若对
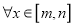 ,
,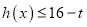 恒成立,求实数t的去取值范围.
恒成立,求实数t的去取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在三棱锥
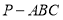 中,已知
中,已知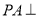 平面
平面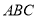 ,
,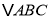 是边长为
是边长为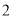 的正三角形,
的正三角形,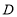 、
、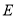 分别为
分别为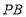 、
、 的中点.
的中点.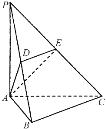
(1)若
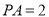 ,求直线
,求直线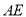 与
与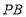 所成角的余弦值;
所成角的余弦值;(2)若平面
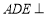 平面
平面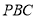 ,求
,求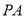 的长.
的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】1852年,英国来华传教士伟烈亚力将《孙子算经》中“物不知数”问题的解法传至欧洲.1874年,英国数学家马西森指出此法符合1801年由高斯得到的关于同余式解法的一般性定理,因而西方称之为“中国剩余定理”.“中国剩余定理”讲的是一个关于整除的问题,例如求1到2000这2000个整数中,能被3除余1且被7除余1的数的个数,现由程序框图,其中MOD函数是一个求余函数,记
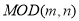 表示m除以n的余数,例如
表示m除以n的余数,例如 ,则输出i为( ).
,则输出i为( ).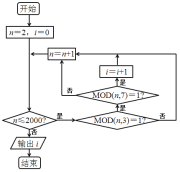
A.98B.97C.96D.95
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知四棱锥
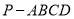 中,底面ABCD是梯形,且
中,底面ABCD是梯形,且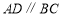 ,
, ,
,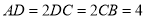 ,
,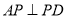 ,
,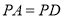 ,
, ,AD的中点为E,则四棱锥
,AD的中点为E,则四棱锥 外接球的表面积为________.
外接球的表面积为________. -
科目: 来源: 题型:
查看答案和解析>>【题目】在新高考改革中,打破了文理分科的“
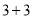 ”模式,不少省份采用了“
”模式,不少省份采用了“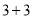 ”,“
”,“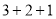 ”,“
”,“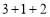 ”等模式.其中“
”等模式.其中“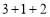 ”模式的操作又更受欢迎,即语数外三门为必考科目,然后在物理和历史中选考一门,最后从剩余的四门中选考两门.某校为了了解学生的选科情况,从高二年级的2000名学生(其中男生1100人,女生900人)中,采用分层抽样的方法从中抽取n名学生进行调查.
”模式的操作又更受欢迎,即语数外三门为必考科目,然后在物理和历史中选考一门,最后从剩余的四门中选考两门.某校为了了解学生的选科情况,从高二年级的2000名学生(其中男生1100人,女生900人)中,采用分层抽样的方法从中抽取n名学生进行调查.(1)已知抽取的n名学生中含男生110人,求n的值及抽取到的女生人数;
(2)在(1)的情况下对抽取到的n名同学“选物理”和“选历史”进行问卷调查,得到下列2×2列联表.请将列联表补充完整,并判断是否有99%的把握认为选科目与性别有关?
选物理
选历史
合计
男生
90
女生
30
合计
(3)在(2)的条件下,从抽取的“选历史”的学生中按性别分层抽样再抽取5名,再从这5名学生中抽取2人了解选政治、地理、化学、生物的情况,求2人至少有1名男生的概率.
参考公式:
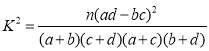 .
.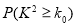
0.10
0.010
0.001
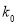
2.706
6.635
10.828
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知直四棱柱
 的底面ABCD是菱形,
的底面ABCD是菱形,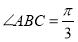 ,E是
,E是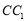 上任意一点.
上任意一点.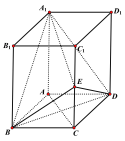
(1)求证:平面
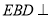 平面
平面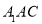 ;
;(2)设
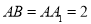 ,当E为
,当E为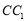 的中点时,求点E到平面
的中点时,求点E到平面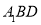 的距离.
的距离.
相关试题

