【题目】有甲、乙两个班级进行数学考试,按照大于等于85分为优秀,85分以下为非优秀统计成绩后,得到如下的列联表.
已知从全部105人中随机抽取1人为优秀的概率为![]() .
.
(1)请完成上面的列联表:若按![]() 的可靠性要求,根据列联表的数据,能否认为“成绩与班级有关系”;
的可靠性要求,根据列联表的数据,能否认为“成绩与班级有关系”;
(2)若按下面的方法从甲班优秀的学生中抽取一人:把甲班优秀的10名学生从2到11进行编号,先后两次抛掷一枚均匀的骰子,出现的点数之和为被抽取人的序号.试求抽到10号的概率.

附: 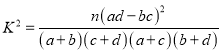

参考答案:
【答案】(1)有![]() 的把握(2)
的把握(2)![]()
【解析】试题分析:
(1)首先写出列联表,利用公式求得![]() ,因此有
,因此有![]() 的把握认为“成绩与班级有关系”.
的把握认为“成绩与班级有关系”.
(2)利用题意可知该事件为古典概型,然后利用古典概型公式求得![]() .
.
试题解析:
(1)
优秀 | 非优秀 | 总计 | |
甲班 | 10 | 45 | 55 |
乙班 | 20 | 30 | 50 |
合计 | 30 | 75 | 105 |
根据列联表中的数据,得到![]()
![]()
因此有![]() 的把握认为“成绩与班级有关系”.
的把握认为“成绩与班级有关系”.
(2)设“抽到10号”为事件![]() ,先后两次抛掷一枚均匀的骰子,出现的点数为
,先后两次抛掷一枚均匀的骰子,出现的点数为![]() ,则所有的基本事件有
,则所有的基本事件有![]() 、
、![]() 、
、![]() 、…、
、…、![]() ,共6个.事件
,共6个.事件![]() 包含的基本事件有
包含的基本事件有![]() ,
, ![]() ,
, ![]() ,共3个,
,共3个,
![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系
 中,曲线
中,曲线 的参数方程为
的参数方程为 (
( 为参数),在以原点为极点,
为参数),在以原点为极点,  轴正半轴为极轴的极坐标系中,直线
轴正半轴为极轴的极坐标系中,直线 的极坐标方程为
的极坐标方程为 .
.(1)求曲线
 的普通方程和直线
的普通方程和直线 的倾斜角;
的倾斜角;(2)设点
 ,直线
,直线 和曲线
和曲线 交于
交于 两点,求
两点,求 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
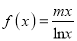 ,曲线
,曲线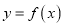 在点
在点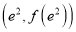 处的切线与直线
处的切线与直线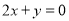 垂直(其中
垂直(其中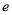 为自然对数的底数).
为自然对数的底数).(I)求
 的解析式及单调递减区间;
的解析式及单调递减区间;(II)是否存在常数
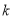 ,使得对于定义域内的任意
,使得对于定义域内的任意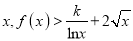 恒成立?若存在,求出
恒成立?若存在,求出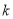 的值;若不存在,请说明理由.
的值;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】在北京召开的国际数学家大会会标如图所示,它是由4个相同的直角三角形与中间的小正方形拼成的一大正方形,若直角三角形中较小的锐角为θ,大正方形的面积是1,小正方形的面积是
 ,则sin2θ﹣cos2θ的值等于( )
,则sin2θ﹣cos2θ的值等于( ) 
A.1
B.﹣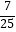
C.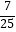
D.﹣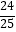
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系
 中,曲线
中,曲线 的参数方程为
的参数方程为 (
( 为参数),在以原点为极点,
为参数),在以原点为极点,  轴正半轴为极轴的极坐标系中,直线
轴正半轴为极轴的极坐标系中,直线 的极坐标方程为
的极坐标方程为 .
.(1)求曲线
 的普通方程和直线
的普通方程和直线 的倾斜角;
的倾斜角;(2)设点
 ,直线
,直线 和曲线
和曲线 交于
交于 两点,求
两点,求 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知向量
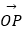 =(2,1),
=(2,1), 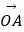 =(1,7),
=(1,7), 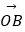 =(5,1),设X是直线OP上的一点(O为坐标原点),那么
=(5,1),设X是直线OP上的一点(O为坐标原点),那么 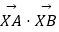 的最小值是 .
的最小值是 . -
科目: 来源: 题型:
查看答案和解析>>【题目】设关于
 的一元二次方程
的一元二次方程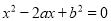 .
.(1)若
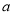 是从0,1,2,3四个数中任取的一个数,
是从0,1,2,3四个数中任取的一个数, 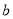 是从0,1,2三个数中任取的一个数,求上述方程有实根的概率;
是从0,1,2三个数中任取的一个数,求上述方程有实根的概率;(2)若
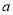 时从区间
时从区间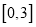 上任取的一个数,
上任取的一个数, 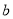 是从区间
是从区间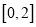 上任取的一个数,求上述方程有实根的概率.
上任取的一个数,求上述方程有实根的概率.
相关试题

