【题目】设关于![]() 的一元二次方程
的一元二次方程![]() .
.
(1)若![]() 是从0,1,2,3四个数中任取的一个数,
是从0,1,2,3四个数中任取的一个数, ![]() 是从0,1,2三个数中任取的一个数,求上述方程有实根的概率;
是从0,1,2三个数中任取的一个数,求上述方程有实根的概率;
(2)若![]() 时从区间
时从区间![]() 上任取的一个数,
上任取的一个数, ![]() 是从区间
是从区间![]() 上任取的一个数,求上述方程有实根的概率.
上任取的一个数,求上述方程有实根的概率.
参考答案:
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】试题分析:由二次方程有实数根可得![]() 满足的条件
满足的条件![]() ,(Ⅰ)中由
,(Ⅰ)中由![]() 可以取得值得到所有基本事件个数及满足条件的基本事件个数,求其比值可求概率;(Ⅱ)中由
可以取得值得到所有基本事件个数及满足条件的基本事件个数,求其比值可求概率;(Ⅱ)中由![]() 范围得到
范围得到![]() 对应的区域,并求得满足
对应的区域,并求得满足![]() 的区域,求其面积比可求其概率
的区域,求其面积比可求其概率
试题解析:设事件![]() 为“方程
为“方程![]() 有实数根”.
有实数根”.
当![]() 时,因为方程
时,因为方程![]() 有实数根,
有实数根,
则![]()
(Ⅰ)基本事件共12个,如下:(0,0),(0,1),(0,2),(1,0),(1,1),(1,2),(2,0),(2,1),(2,2),(3,0),(3,1),(3,2)其中第一个数表示![]() 的取值,第二个数表示
的取值,第二个数表示![]() 的取值,事件
的取值,事件![]() 包含9个基本事件,事件
包含9个基本事件,事件![]() 发生的概率为
发生的概率为![]()
(Ⅱ)实验的全部结果所构成的区域为![]() ,
,
构成事件![]() 的区域为
的区域为![]()
所以所求的概率为: 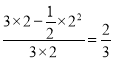
-
科目: 来源: 题型:
查看答案和解析>>【题目】有甲、乙两个班级进行数学考试,按照大于等于85分为优秀,85分以下为非优秀统计成绩后,得到如下的列联表.
已知从全部105人中随机抽取1人为优秀的概率为
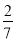 .
.(1)请完成上面的列联表:若按
 的可靠性要求,根据列联表的数据,能否认为“成绩与班级有关系”;
的可靠性要求,根据列联表的数据,能否认为“成绩与班级有关系”;(2)若按下面的方法从甲班优秀的学生中抽取一人:把甲班优秀的10名学生从2到11进行编号,先后两次抛掷一枚均匀的骰子,出现的点数之和为被抽取人的序号.试求抽到10号的概率.

附:
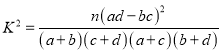

-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系
 中,曲线
中,曲线 的参数方程为
的参数方程为 (
( 为参数),在以原点为极点,
为参数),在以原点为极点,  轴正半轴为极轴的极坐标系中,直线
轴正半轴为极轴的极坐标系中,直线 的极坐标方程为
的极坐标方程为 .
.(1)求曲线
 的普通方程和直线
的普通方程和直线 的倾斜角;
的倾斜角;(2)设点
 ,直线
,直线 和曲线
和曲线 交于
交于 两点,求
两点,求 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知向量
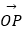 =(2,1),
=(2,1), 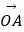 =(1,7),
=(1,7), 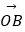 =(5,1),设X是直线OP上的一点(O为坐标原点),那么
=(5,1),设X是直线OP上的一点(O为坐标原点),那么 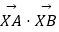 的最小值是 .
的最小值是 . -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四棱锥
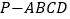 中,
中,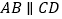 ,
,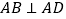 ,
,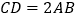 ,平面
,平面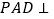 平面
平面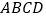 ,
,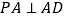 .
.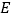 和
和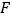 分别是
分别是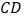 和
和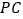 的中点.
的中点.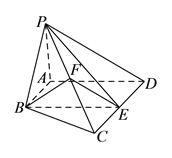
求证:(I)
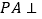 底面
底面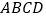 .
.(II)平面
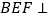 平面
平面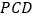 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】在四棱柱
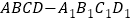 中,
中,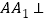 底面
底面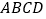 ,底面
,底面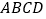 为菱形,
为菱形,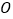 为
为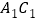 与
与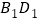 交点,已知
交点,已知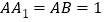 ,
,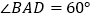 .
.(I)求证:
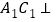 平面
平面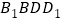 .
.(II)在线段
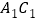 上是否存在一点
上是否存在一点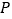 ,使得
,使得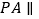 平面
平面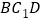 ,如果存在,求
,如果存在,求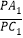 的值,如果不存在,请说明理由.
的值,如果不存在,请说明理由.(III)设点
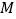 在
在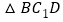 内(含边界),且
内(含边界),且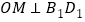 ,求所有满足条件的点
,求所有满足条件的点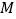 构成的图形,并求
构成的图形,并求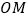 的最小值.
的最小值.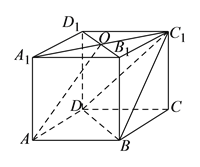
-
科目: 来源: 题型:
查看答案和解析>>【题目】若存在实数
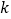 和
和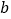 ,使得函数
,使得函数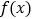 和
和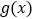 对定义域内的任意
对定义域内的任意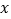 均满足:
均满足: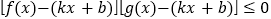 ,且存在
,且存在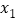 使得
使得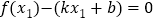 ,存在
,存在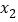 使得
使得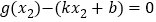 ,则称直线
,则称直线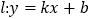 为函数
为函数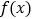 和
和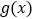 的“分界线”.在下列说法中正确的是__________(写出所有正确命题的编号).
的“分界线”.在下列说法中正确的是__________(写出所有正确命题的编号).①任意两个一次函数最多存在一条“分界线”;
②“分界线”存在的两个函数的图象最多只有两个交点;
③
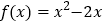 与
与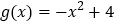 的“分界线”是
的“分界线”是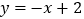 ;
;④
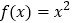 与
与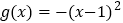 的“分界线”是
的“分界线”是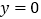 或
或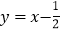 .
.
相关试题

