【题目】已知函数f(x)=![]()
![]() (t+1)lnx,,其中t∈R.
(t+1)lnx,,其中t∈R.
(1)若t=1,求证:当x>1时,f(x)>0成立;
(2)若t>![]() ,判断函数g(x)=x[f(x)+t+1]的零点的个数.
,判断函数g(x)=x[f(x)+t+1]的零点的个数.
参考答案:
【答案】(1)见解析(2)1
【解析】试题分析:(1)当![]() 时,对
时,对![]() 求导,
求导, ![]() 得增区间,
得增区间,![]() 得减区间,进而求出函数的最小值值,即可证明;(2)若t>
得减区间,进而求出函数的最小值值,即可证明;(2)若t>![]() ,求得函数g(x)=x[f(x)+t+1]的导函数,研究其单调性,根据零点定理再利用导数即可判定零点的个数.
,求得函数g(x)=x[f(x)+t+1]的导函数,研究其单调性,根据零点定理再利用导数即可判定零点的个数.
试题解析:解:(1)t=1时,f(x)=x﹣![]() ﹣2lnx,x>0
﹣2lnx,x>0
∴f′(x)=1+![]() ﹣
﹣![]() =
=![]() =
=![]() ≥0,
≥0,
∴f(x)在(1,+∞)上单调递增,
∴f(x)>f(1)=1﹣1﹣0=0,
∴x>1,f(x)>0成立,
(2)当x∈(0,+∞),g(x)=tx2﹣(t+1)xlnx+(t+1)x﹣1
∴g′(x)=2tx﹣(t+1)lnx,
设m(x)=2tx﹣(t+1)lnx, ∴m′(x)=2t﹣![]() =
=![]() ,
,
令m′(x)=0,得x=![]() ,
,
当0<x<![]() 时,m'(x)<0;当时x>
时,m'(x)<0;当时x>![]() ,m'(x)>0.
,m'(x)>0.
∴g'(x)在(0,![]() )上单调递减,在(
)上单调递减,在(![]() ,+∞)上单调递增.
,+∞)上单调递增.
∴g'(x)的最小值为g′(![]() )=(t+1)(1﹣ln
)=(t+1)(1﹣ln![]() ),
),
∵t>![]() ,∴
,∴![]() =
=![]() +
+![]() <
<![]() +
+![]() <e.
<e.
∴g'(x)的最小值g′(![]() )=(t+1)(1﹣ln
)=(t+1)(1﹣ln![]() )>0,
)>0,
从而,g(x)在区间(0,+∞)上单调递增.
又g(1)=2t>0,又g(![]() )=
)=![]() +
+![]() (6+2lnt)﹣1,
(6+2lnt)﹣1,
设h(t)=e3t﹣(2lnt+6).
则h′(t)=e3﹣![]() .
.
令h'(t)=0得t=![]() .由h'(t)<0,得0<t<
.由h'(t)<0,得0<t<![]() ;
;
由h'(t)>0,得t>![]() .
.
∴h(t)在(0,![]() )上单调递减,在(
)上单调递减,在(![]() ,+∞)上单调递增.
,+∞)上单调递增.
∴h(t)min=h(![]() )=2﹣2ln2>0.
)=2﹣2ln2>0.
∴h(t)>0恒成立.∴e3t>2lnt+6,.
∴g(![]() )<
)<![]() +
+![]() ﹣1=
﹣1=![]() +
+![]() +
+![]() ﹣1<
﹣1<![]() +
+![]() +
+![]() ﹣1<0.
﹣1<0.
∴当t>![]() 时,函数g(x)恰有1个零点
时,函数g(x)恰有1个零点
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线
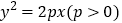 ,过点
,过点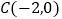 的直线
的直线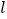 交抛物线于
交抛物线于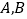 两点,坐标原点为
两点,坐标原点为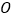 ,且
,且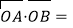 12.
12.(Ⅰ)求抛物线的方程;
(Ⅱ)当以
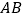 为直径的圆的面积为
为直径的圆的面积为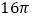 时,求
时,求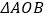 的面积
的面积 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知p:x∈A={x|x2﹣2x﹣3≤0,x∈R},q:x∈B={x|x2﹣2mx+m2﹣9≤0,x∈R,m∈R}.
(1)若A∩B=[1,3],求实数m的值;
(2)若p是q的充分条件,求实数m的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知一次函数f(x)为增函数,且f(f(x))=4x+9,g(x)=mx+m+3(m∈R).
(1)当x∈[-1,2]时,若不等式g(x)>0恒成立,求m的取值范围;
(2)如果函数F(x)=f(x)g(x)为偶函数,求m的值;
(3)当函数f(x)和g(x)满足f(g(x))=g(f(x))时,求函数
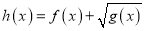 的值域.
的值域. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线
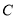 :
:  的焦点为
的焦点为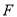 ,点
,点 为其上一点,且
为其上一点,且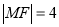 .
.(1)求
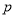 与
与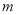 的值;
的值;(2)如图,过点
 作直线
作直线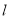 交抛物线于
交抛物线于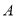 、
、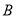 两点,求直线
两点,求直线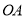 、
、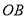 的斜率之积.
的斜率之积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两家商场对同一种商品开展促销活动,对购买该商品的顾客两家商场的奖励方案如下:
甲商场:顾客转动如图所示圆盘,当指针指向阴影部分(图中两个阴影部分均为扇形,且每个扇形圆心角均为
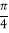 ,边界忽略不计)即为中奖·
,边界忽略不计)即为中奖·乙商场:从装有2个白球、2个蓝球和2个红球的盒子中一次性摸出1球(这些球除颜色外完全相同),它是红球的概率是
 ,若从盒子中一次性摸出2球,且摸到的是2个相同颜色的球,即为中奖.
,若从盒子中一次性摸出2球,且摸到的是2个相同颜色的球,即为中奖.
(Ⅰ)求实数
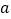 的值;
的值;(Ⅱ)试问:购买该商品的顾客在哪家商场中奖的可能性大?请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】选修
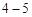 :不等式选讲
:不等式选讲已知函数f(x)=|2x+3|+|2x﹣1|.
(Ⅰ)求不等式f(x)<8的解集;
(Ⅱ)若关于x的不等式f(x)≤|3m+1|有解,求实数m的取值范围.
相关试题

