Question

【题目】已知数列{an}前n项和为Sn ， 满足Sn=2an﹣2n（n∈N*）．
（1）证明：{an+2}是等比数列，并求{an}的通项公式；
（2）数列{bn}满足bn=log2（an+2），Tn为数列{ }的前n项和，若Tn＜a对正整数a都成立，求a的取值范围．

Answer 1

【答案】
（1）证明：由题设Sn=2an﹣2n（n∈N*），

Sn﹣1=2an﹣1﹣2（n﹣1），n≥2，

两式相减得an=2an﹣1+2，

即an+2=2（an﹣1+2），

又a1+2=4，

所以{an+2}是以4为首项，2为公比的等比数列，

an+2=42n﹣1，即an=2n+1﹣2（n≥2）

又a1=2，所以an=2n+1﹣2（n∈N*）；

（2）解：因为bn=log2（an+2）=log22n+1=n+1，

即有 = = ﹣ ，

故Tn= ﹣ + ﹣ +…+ ﹣ = ﹣ ＜ ，

依题意得：a≥

【解析】（1）运用数列的通项和前n项和的关系，变形整理即可得到{an+2}是等比数列，由等比数列的通项公式，即可求得；（2）运用对数的运算性质，化简bn ， 再由裂项相消求和，即可得到Tn ， 运用不等式恒成立思想即可得到a的范围．
【考点精析】解答此题的关键在于理解数列的前n项和的相关知识，掌握数列{an}的前n项和sn与通项an的关系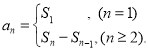，以及对数列的通项公式的理解，了解如果数列an的第n项与n之间的关系可以用一个公式表示，那么这个公式就叫这个数列的通项公式．