Question

【题目】设函数f（x）=|2x﹣1|﹣|x+2|．
（1）解不等式f（x）＞3；
（2）若x0∈R，使得f（x0）+2m2＜4m，求实数m的取值范围．

Answer 1

【答案】
（1）解：当x＜﹣2时，f（x）=|2x﹣1|﹣|x+2|=1﹣2x+x+2=﹣x+3，f（x）＞3，即﹣x+3＞3，解得x＜0，

又x＜﹣2，∴x＜﹣2；

当 时，f（x）=|2x﹣1|﹣|x+2|=1﹣2x﹣x﹣2=﹣3x﹣1，f（x）＞3，即﹣3x﹣1＞3，解得 ，又 ，∴ ；

当 时，f（x）=|2x﹣1|﹣|x+2|=2x﹣1﹣x﹣2=x﹣3，f（x）＞3，即x﹣3＞3，解得x＞6，又 ，∴x＞6．

综上，不等式f（x）＞3的解集为 ．

（2）解：f（x）=|2x﹣1|﹣|x+2|= ，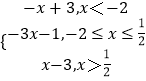

∴ ．

∵x0∈R，使得 ，

∴ ，

整理得4m2﹣8m﹣5＜0，

解得 ．

因此实数m的取值范围是

【解析】（1）利用零点分区间讨论去掉绝对值符号，化为分段函数，在每一个前提下去解不等式，每一步的解都要和前提条件找交集得出每一步的解，最后把每一步最后结果找并集得出不等式的解；（2）根据第一步所化出的分段函数求出函数f（x）的最小值，若x0∈R，使得f（x0）+2m2＜4m成立，只需4m﹣2m2＞fmin（x），解出实数m的取值范围．
【考点精析】本题主要考查了绝对值不等式的解法的相关知识点，需要掌握含绝对值不等式的解法：定义法、平方法、同解变形法，其同解定理有；规律：关键是去掉绝对值的符号才能正确解答此题．