【题目】已知函数![]() ,
, ![]()
![]() ,记
,记
![]() 。
。
(1) 判断的奇偶性(不用证明)并写出的单调区间;
(2)若![]() 对于一切
对于一切![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
(3)对任意![]() ,都存在
,都存在![]() ,使得
,使得![]() ,
, ![]() .若
.若![]() ,求实数
,求实数![]() 的值;
的值;
参考答案:
【答案】(1)奇函数,在R上单调递增(2)![]() (3)
(3)![]()
【解析】试题分析:(1)利用奇偶性的定义判断函数的奇偶性,利用复合函数的单调性性质写出单调区间;(2)含参数的恒成立问题采用分离参数法,得到![]() ,解得
,解得![]() ,
, ![]() 的最大值,则
的最大值,则![]() 即可;(3)由题意可知,
即可;(3)由题意可知, ![]() ,
, ![]() ,所以
,所以![]() ,解得
,解得![]() 。
。
试题解析:
(Ⅰ)函数![]() 为奇函数,在R上单调递增
为奇函数,在R上单调递增
(Ⅱ)当![]() 时,
时, ![]()
即![]() ,
,
![]() ,
, ![]()
令![]() ,
, ![]()
下面求函数![]() 的最大值。
的最大值。
![]() ,
, ![]()
∴![]()
故![]() 的取值范围是
的取值范围是![]()
(Ⅲ)据题意知,当![]() 时,
时, ![]() ,
, ![]()
∵![]() 在区间
在区间![]() 上单调递增,
上单调递增,
∴![]() ,即
,即![]()
又∵![]()
∴函数![]() 的对称轴为
的对称轴为![]()
∴函数![]() 在区间
在区间![]() 上单调递减
上单调递减
∴![]() ,即
,即![]()
由![]() ,得
,得![]() ,
,
∴![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了预防流感,某学校对教室用药熏消毒法进行消毒,已知药物释放过程中,室内每立方米空气中的含药量y(毫克)与时间t(小时)成正比;药物释放完毕后,y与t的函数关系式为
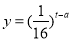 (a为常数),如图所示.根据图中提供的信息,回答下列问题:
(a为常数),如图所示.根据图中提供的信息,回答下列问题:
(1)从药物释放开始,每立方米空气中的含药量y(毫克)与时间t(小时)之间的函数关系式为_________;
(2)据测定,当空气中每立方米的含药量降低到0.25毫克以下时,学生方可进教室,那么从药物释放开始,至少需要经过_________小时后,学生才能回到教室.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四棱锥
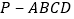 中,已知
中,已知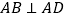 ,
,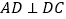 ,
,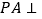 底面
底面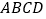 ,且
,且 ,
,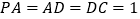 ,
,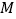 为
为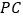 的中点,
的中点, 在
在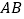 上,且
上,且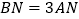 .
.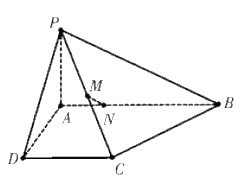
(1)求证:平面
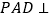 平面
平面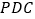 ;
;(2)求证:
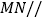 平面
平面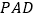 ;
;(3)求三棱锥
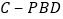 的体积.
的体积. -
科目: 来源: 题型:
查看答案和解析>>【题目】某电脑公司在甲、乙两地各有一个分公司,甲分公司现有电脑6台,乙分公司现有同一型号的电脑12台.现A地某单位向该公司购买该型号的电脑10台,B地某单位向该公司购买该型号的电脑8台.已知从甲地运往A,B两地每台电脑的运费分别是40元和30元,从乙地运往A,B两地每台电脑的运费分别是80元和50元. 若总运费不超过1000元,则调运方案的种数为
A.1 B.2
C.3 D.4
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知向量
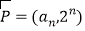 ,
,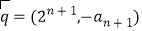 ,
,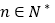 ,向量
,向量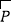 与
与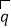 垂直,且
垂直,且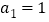 .
.(1)求数列
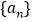 的通项公式;
的通项公式;(2)若数列
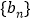 满足
满足 ,求数列
,求数列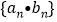 的前
的前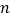 项和
项和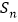 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知
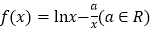 .
.(1)若函数
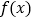 的图象在点
的图象在点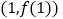 处的切线平行于直线
处的切线平行于直线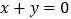 ,求
,求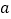 的值;
的值;(2)讨论函数
 在定义域上的单调性;
在定义域上的单调性;(3)若函数
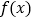 在
在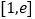 上的最小值为
上的最小值为 ,求
,求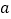 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】某高校共有15000人,其中男生10500人,女生4500人,为调查该校学生每周平均体育运动时间的情况,采用分层抽样的方法,收集300位学生每周平均体育运动时间的样本数据(单位:小时)
(Ⅰ)应收集多少位女生样本数据?
(Ⅱ)根据这300个样本数据,得到学生每周平均体育运动时间的频率分布直方图(如图所示),其中样本数据分组区间为:
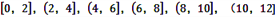 .估计该校学生每周平均体育运动时间超过4个小时的概率.
.估计该校学生每周平均体育运动时间超过4个小时的概率. 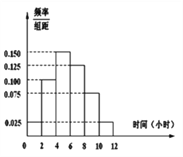
(Ⅲ)在样本数据中,有60位女生的每周平均体育运动时间超过4个小时.请完成每周平均体育运动时间与性别的列联表,并判断是否有
 的把握认为“该校学生的每周平均体育运动时间与性别有关”.
的把握认为“该校学生的每周平均体育运动时间与性别有关”.附:
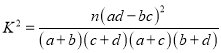
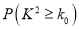
0.10
0.05
0.010
0.005
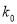
2.706
3.841
6.635
7.879
相关试题

