【题目】设函数![]() ,
,![]() .
.
(1)若函数![]() 在
在![]() 处有极值,求函数
处有极值,求函数![]() 的最大值;
的最大值;
(2)①是否存在实数![]() ,使得关于
,使得关于![]() 的不等式
的不等式![]() 在
在![]() 上恒成立?若存在,求出
上恒成立?若存在,求出![]() 的取值范围;若不存在,说明理由;
的取值范围;若不存在,说明理由;
②证明:不等式![]() .
.
参考答案:
【答案】(1)![]() ;(2)①
;(2)①![]() ;②证明见解析.
;②证明见解析.
【解析】
试题分析:(1)由![]() 的解,即可得出极值点,得出
的解,即可得出极值点,得出![]() 值后,再利用导函数求单调区间;(2)①本题为恒成立问题,利用函数的增减性和端点值来求解,而函数的单调性由导函数的正负来决定;②运用不等式的放缩与基本不等式的性质,证明右边项时采用了数列的增减性的基本定义来证明,通过说明数列时单调递减来证明不等式,在证明右侧时,采用将
值后,再利用导函数求单调区间;(2)①本题为恒成立问题,利用函数的增减性和端点值来求解,而函数的单调性由导函数的正负来决定;②运用不等式的放缩与基本不等式的性质,证明右边项时采用了数列的增减性的基本定义来证明,通过说明数列时单调递减来证明不等式,在证明右侧时,采用将![]() 裂项的方法,将详见得到的每一项放缩,最后利用裂项相消
裂项的方法,将详见得到的每一项放缩,最后利用裂项相消![]() 来证得不等式成立.
来证得不等式成立.
试题解析:解:(1)由已知得:![]() ,且函数
,且函数![]() 在
在![]() 处有极值
处有极值
∴![]() ,即
,即![]() ,∴
,∴![]()
∴![]() .
.
当![]() 时,
时,![]() ,
,![]() 单调递增;
单调递增;
当![]() 时,
时,![]() ,
,![]() 单调递减,
单调递减,
∴函数![]() 的最大值为
的最大值为![]() .
.
(2)①由已知得:![]()
(ⅰ)若![]() ,则
,则![]() 时,
时,![]()
∴![]() 在
在![]() 上为减函数,
上为减函数,
∴![]() 在
在![]() 上恒成立;
上恒成立;
(ⅱ)若![]() ,则
,则![]() 时,
时,![]()
∴![]() 在
在![]() 上为增函数,
上为增函数,
∴![]() ,不能使
,不能使![]() 在
在![]() 上恒成立;
上恒成立;
(ⅲ)若![]() ,则
,则![]() 时,
时,![]() ,
,
当![]() 时,
时,![]() ,∴
,∴![]() 在
在![]() 上为增函数,
上为增函数,
此时![]() ,∴不能使
,∴不能使![]() 在
在![]() 上恒成立;
上恒成立;
综上所述,![]() 的取值范围是
的取值范围是![]() .
.
②由以上得:![]()
取![]() 得:
得:![]() ,令
,令![]() ,
,
则![]() ,
,![]() .
.
因此![]()
又![]()
故![]()
![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
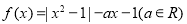 .
.(1)若关于
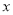 的方程
的方程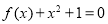 在区间
在区间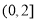 上有两个不同的解
上有两个不同的解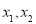 .
.(ⅰ)求
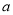 的取值范围;
的取值范围;(ⅱ)若
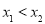 ,求
,求 的取值范围;
的取值范围;(2)设函数
 在区间
在区间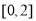 上的最大值和最小值分别为
上的最大值和最小值分别为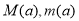 ,求
,求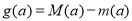 的表达式.
的表达式. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠C=90°,D,E分别为AC,AB的中点,点F为线段CD上的一点.将△ADE沿DE折起到△A1DE的位置,使A1F⊥CD,如图2.
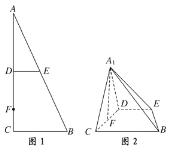
(1)求证:DE∥平面A1CB;
(2)求证:A1F⊥BE;
(3)线段A1B上是否存在点Q,使A1C⊥平面DEQ?说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】设函数
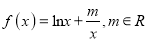 .
.(1)当
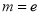 (
(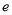 为自然对数的底数)时,求
为自然对数的底数)时,求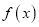 的最小值;
的最小值;(2)讨论函数
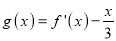 零点的个数;
零点的个数;(3)若对任意
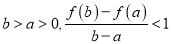 恒成立,求
恒成立,求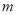 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,在四棱锥P-ABCD中,底面是边长为a的正方形,侧棱PD=a,PA=PC=
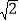 a,
a,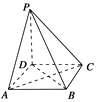
(1)求证:PD⊥平面ABCD;
(2)求证:平面PAC⊥平面PBD;
(3)求二面角P-AC-D的正切值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四棱锥P-ABCD中,平面PAD⊥平面ABCD,AB=AD,∠BAD=60°,E,F分别是AP,AD的中点.
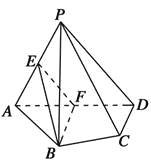
求证:(1)直线EF∥平面PCD;
(2)平面BEF⊥平面PAD.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
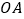 、
、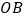 是两条公路(近似看成两条直线),
是两条公路(近似看成两条直线),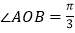 ,在
,在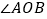 内有一纪念塔
内有一纪念塔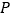 (大小忽略不计),已知
(大小忽略不计),已知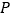 到直线
到直线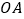 、
、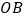 的距离分别为
的距离分别为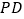 、
、 ,
,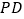 =6千米,
=6千米, =12千米.现经过纪念塔
=12千米.现经过纪念塔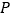 修建一条直线型小路,与两条公路
修建一条直线型小路,与两条公路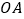 、
、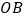 分别交于点
分别交于点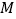 、
、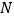 .
.(1)求纪念塔
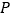 到两条公路交点
到两条公路交点 处的距离;
处的距离;(2)若纪念塔
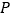 为小路
为小路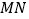 的中点,求小路
的中点,求小路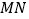 的长.
的长.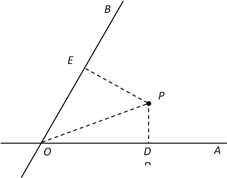
相关试题

