《2025年新课标两导两练高效学案四年级数学上册人教版》

3. 过点$B画AC$的垂线。

答案： 答题卡：
(1)
使用三角尺的一条直角边与$AC$重合，
平移三角尺使另一条直角边经过点$B$，
沿这条直角边画直线，所画直线即为过点$B$的$AC$的垂线。
(2)
使用三角尺的一条直角边与$AC$重合，
移动三角尺使另一条直角边经过点$B$，
沿直角边画直线，该直线就是过点$B$的$AC$的垂线。
(3)
使用三角尺的一条直角边与$AC$重合（需要延长$AC$），
移动三角尺使另一条直角边经过点$B$，
沿直角边画直线，此直线为过点$B$的$AC$的垂线。

4. 如图,直线$l_1 // l_2$、$l_3 // l_4$,已知$\angle 1 + \angle 2 = 180°$,不测量,你能说明$\angle 2$、$\angle 3$、$\angle 4$、$\angle 5$的关系吗？

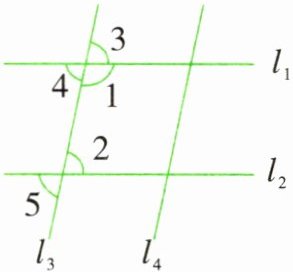
答案： ∠2=∠3=∠4=∠5。
步骤：
1.
∵∠1与∠3是邻补角（平角定义），
∴∠1+∠3=180°。
2.
∵∠1+∠2=180°（已知），
∴∠3=∠2（同角的补角相等）。
3.
∵l₃//l₄，l₁为截线，∠3与∠4是同位角，
∴∠3=∠4（两直线平行，同位角相等），故∠4=∠2。
4.
∵l₁//l₂，l₃为截线，∠2与∠5是内错角，
∴∠2=∠5（两直线平行，内错角相等）。
综上，∠2=∠3=∠4=∠5。