第25页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
例1 工程队要修一条小路,第一天修了全长的一半多20米,第二天修了余下的一半少20米,第三天修了40米,此时还剩下10米没有修,这条小路长多少米?
答案:
160÷2 80 - 20 60÷2 30 + 20 50 - 40 10
×2 + 20 ×2 - 20 + 40
剩下 10米
余下的一半 40 - 20 + 10 = 30(米)
余下的 30×2 = 60(米)
全长的一半 60 + 20 = 80(米)
全长 80×2 = 160(米)
×2 + 20 ×2 - 20 + 40
剩下 10米
余下的一半 40 - 20 + 10 = 30(米)
余下的 30×2 = 60(米)
全长的一半 60 + 20 = 80(米)
全长 80×2 = 160(米)
方法一:画火车图
①“一半”型:用去一半,剩下一半,故用□÷2表示剩下的数量;
②“一半多几”型:用去一半多几,剩下一半少几,故用□÷2再减几表示剩下的数量;
③“一半少几”型:用去一半少几,剩下一半多几,故用□÷2再加几表示剩下的数量。
第一步:画出“剩下情况”的火车图。
□÷2→□-20→□÷2→□+20→□-40→10
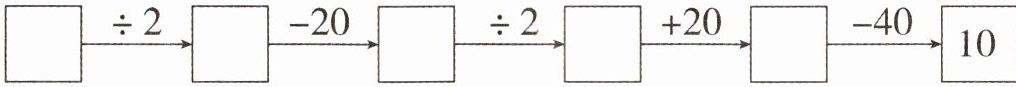
第二步:从结果出发倒推,+、-互逆,×、÷互逆。亲爱的小朋友,请你根据本题的火车图,完成倒推计算。

方法二:画线段图
我们可以根据线段图理清数量关系,从剩下的10米出发,第一次倒推第一天修后余下的一半,第二次倒推小路全长的一半,如下图(单位:米)。
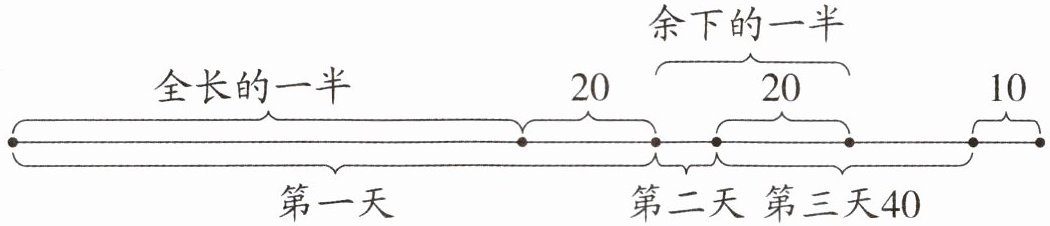
亲爱的小朋友,请你根据线段图填表列式计算:
| 剩下 | 10 米 |
| 余下的一半 |
| 余下的 |
| 全长的一半 |
| 全长 |


①“一半”型:用去一半,剩下一半,故用□÷2表示剩下的数量;
②“一半多几”型:用去一半多几,剩下一半少几,故用□÷2再减几表示剩下的数量;
③“一半少几”型:用去一半少几,剩下一半多几,故用□÷2再加几表示剩下的数量。
第一步:画出“剩下情况”的火车图。
□÷2→□-20→□÷2→□+20→□-40→10
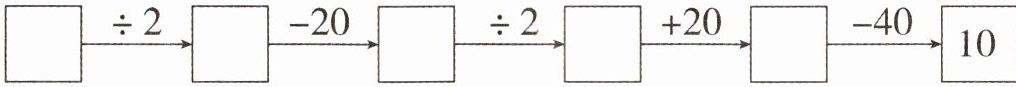
第二步:从结果出发倒推,+、-互逆,×、÷互逆。亲爱的小朋友,请你根据本题的火车图,完成倒推计算。

160
←÷2→80
←+20→60
←÷2→30
←-20→50
←+40→10方法二:画线段图
我们可以根据线段图理清数量关系,从剩下的10米出发,第一次倒推第一天修后余下的一半,第二次倒推小路全长的一半,如下图(单位:米)。

亲爱的小朋友,请你根据线段图填表列式计算:
| 剩下 | 10 米 |
| 余下的一半 |
50米
|| 余下的 |
100米
|| 全长的一半 |
120米
|| 全长 |
160米
|

答案:
解析:本题可根据题目所给的两种方法(画火车图和画线段图),分别通过倒推的方式计算出小路的全长。
方法一:画火车图
从结果“$10$”出发,根据“$+、-$互逆,$×、÷$互逆”的原则进行倒推。
最后一个运算“$-40$”,其逆运算是“$+40$”,所以$10 + 40 = 50$;
上一个运算是“$+20$”,其逆运算是“$-20$”,所以$50 - 20 = 30$;
再上一个运算是“$÷2$”,其逆运算是“$×2$”,所以$30×2 = 60$;
接着“$-20$”的逆运算是“$+20$”,所以$60 + 20 = 80$;
最开始的“$÷2$”的逆运算是“$×2$”,所以$80×2 = 160$。
方法二:画线段图
从剩下的$10$米出发,第一次倒推第一天修后余下的一半,第二次倒推小路全长的一半。
已知剩下$10$米,这是第三天修完$40$米后剩下的,那么第二天修完剩下的长度为$(10 + 40)×2 = 100$(米);
第一天修完剩下的长度为$(100 + 20)×2 = 240÷2=120×2 = 160$(米),即小路全长为$160$米。
答案:
方法一:
从后往前计算:
$(10 + 40)×2 = 100$;
$(100 - 20)×2 = 160$(米)
方法二:
| 剩下 | $10$米 |
| --- | --- |
| 余下的一半 | $(10 + 40)=50$(米) |
| 余下的 | $50×2 = 100$(米) |
| 全长的一半 | $(100 + 20)=120$(米) |
| 全长 | $120×2 = 160$(米) |
小路全长$160$米。
方法一:画火车图
从结果“$10$”出发,根据“$+、-$互逆,$×、÷$互逆”的原则进行倒推。
最后一个运算“$-40$”,其逆运算是“$+40$”,所以$10 + 40 = 50$;
上一个运算是“$+20$”,其逆运算是“$-20$”,所以$50 - 20 = 30$;
再上一个运算是“$÷2$”,其逆运算是“$×2$”,所以$30×2 = 60$;
接着“$-20$”的逆运算是“$+20$”,所以$60 + 20 = 80$;
最开始的“$÷2$”的逆运算是“$×2$”,所以$80×2 = 160$。
方法二:画线段图
从剩下的$10$米出发,第一次倒推第一天修后余下的一半,第二次倒推小路全长的一半。
已知剩下$10$米,这是第三天修完$40$米后剩下的,那么第二天修完剩下的长度为$(10 + 40)×2 = 100$(米);
第一天修完剩下的长度为$(100 + 20)×2 = 240÷2=120×2 = 160$(米),即小路全长为$160$米。
答案:
方法一:
从后往前计算:
$(10 + 40)×2 = 100$;
$(100 - 20)×2 = 160$(米)
方法二:
| 剩下 | $10$米 |
| --- | --- |
| 余下的一半 | $(10 + 40)=50$(米) |
| 余下的 | $50×2 = 100$(米) |
| 全长的一半 | $(100 + 20)=120$(米) |
| 全长 | $120×2 = 160$(米) |
小路全长$160$米。
查看更多完整答案,请扫码查看


