《2025年快乐暑假每一天四年级》

1. 画出下面各图形所有的对称轴。

（等边三角形有3条对称轴；正方形有4条对称轴；正五边形有5条对称轴；正六边形有6条对称轴）

答案： 本题可根据对称轴的定义，分别找出各图形的对称轴并画出。
步骤一：分析等边三角形的对称轴
等边三角形的三条高所在的直线就是它的对称轴，因为等边三角形三条边相等，三个角也相等，沿着高所在直线对折，直线两侧的部分能够完全重合。所以等边三角形有$3$条对称轴。
步骤二：分析正方形的对称轴
正方形对边中点的连线以及两条对角线所在的直线是它的对称轴。
对边中点连线：正方形两组对边分别相等且平行，对边中点连线所在直线可使正方形沿此直线对折后完全重合，有$2$条。
对角线：正方形的对角线相等且互相垂直平分，沿对角线所在直线对折，直线两侧部分完全重合，有$2$条。
所以正方形共有$4$条对称轴。
步骤三：分析正五边形的对称轴
正五边形顶点与对边中点的连线是它的对称轴。因为正五边形五条边相等，五个角也相等，从每个顶点向对边中点作直线，沿此直线对折，正五边形直线两侧部分能够完全重合，所以正五边形有$5$条对称轴。
步骤四：分析正六边形的对称轴
正六边形的对称轴有两种：
对边中点的连线：正六边形有三组对边，每组对边中点连线所在直线可使正六边形沿此直线对折后完全重合，有$3$条。
对角线：过相对顶点的直线也是对称轴，正六边形有$3$条这样的对角线，沿此直线对折，直线两侧部分完全重合。
所以正六边形共有$6$条对称轴。
根据上述分析，按照对称轴的定义，用直尺分别画出各图形的对称轴（画图略）。
综上，答案依次为：等边三角形$\boldsymbol{3}$条对称轴；正方形$\boldsymbol{4}$条对称轴；正五边形$\boldsymbol{5}$条对称轴；正六边形$\boldsymbol{6}$条对称轴。

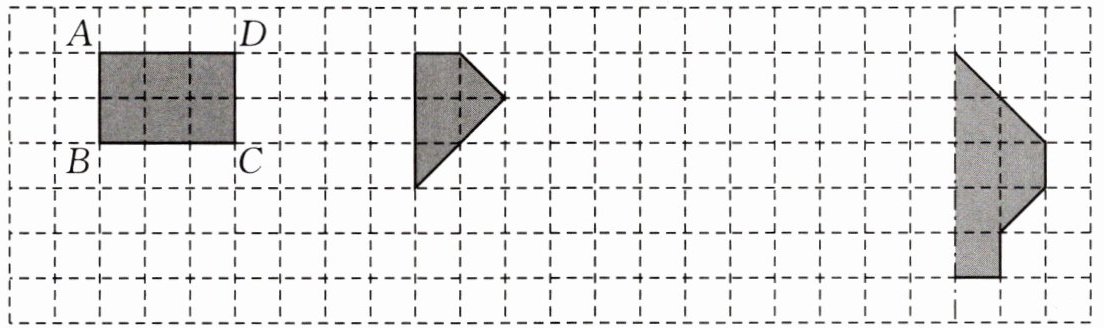
2. (1)将长方形 $ABCD$ 绕点 $C$ 逆时针旋转 $90^{\circ}$,画出旋转后的图形。根据旋转的性质：旋转前后图形的大小和形状没有改变，对应点到旋转中心的距离相等，对应点与旋转中心连线所成的角度等于旋转的角度。先确定长方形$ABCD$的四个顶点$A$、$B$、$C$、$D$绕点$C$逆时针旋转$90^{\circ}$后的对应点$A'$、$B'$、$C$（$C$点旋转后位置不变）、$D'$。然后依次连接$B'C$、$CD'$、$D'A'$、$A'B'$，得到旋转后的长方形。
(2)将中间的图形先向下平移 $3$ 格,再向左平移 $2$ 格,画出平移后的图形。根据平移的性质：平移不改变图形的形状和大小，只改变图形的位置。先将中间图形的每个顶点向下平移$3$格，得到一组新的顶点。再将这组新顶点向左平移$2$格。最后依次连接平移后的顶点，得到平移后的图形。
(3)画出右边图形的另一半,使它成为轴对称图形。根据轴对称图形的性质：轴对称图形沿着对称轴对折后，两边的图形能够完全重合。先确定右边图形的对称轴。然后找出图形各顶点关于对称轴的对称点。最后依次连接对称点，画出图形的另一半。

答案： 本题考查图形的旋转、平移和轴对称图形的绘制，可根据对应图形的性质进行绘制。
$(1)$ 绘制长方形$ABCD$绕点$C$逆时针旋转$90^{\circ}$后的图形
根据旋转的性质：旋转前后图形的大小和形状没有改变，对应点到旋转中心的距离相等，对应点与旋转中心连线所成的角度等于旋转的角度。
先确定长方形$ABCD$的四个顶点$A$、$B$、$C$、$D$绕点$C$逆时针旋转$90^{\circ}$后的对应点$A'$、$B'$、$C$（$C$点旋转后位置不变）、$D'$。
然后依次连接$B'C$、$CD'$、$D'A'$、$A'B'$，得到旋转后的长方形。
$(2)$ 绘制中间图形先向下平移$3$格，再向左平移$2$格后的图形
根据平移的性质：平移不改变图形的形状和大小，只改变图形的位置。
先将中间图形的每个顶点向下平移$3$格，得到一组新的顶点。
再将这组新顶点向左平移$2$格。
最后依次连接平移后的顶点，得到平移后的图形。
$(3)$ 绘制右边图形的另一半，使它成为轴对称图形
根据轴对称图形的性质：轴对称图形沿着对称轴对折后，两边的图形能够完全重合。
先确定右边图形的对称轴。
然后找出图形各顶点关于对称轴的对称点。
最后依次连接对称点，画出图形的另一半。
由于本题是绘图题，无法直接展示图形，你可以根据上述步骤进行绘制。
综上，按照图形变换的性质完成$\boldsymbol{(1)}$ **长方形旋转**、$\boldsymbol{(2)}$ **中间图形平移**、$\boldsymbol{(3)}$ **右边图形补全轴对称图形**的绘制 。

$A$、$B$、$C$、$D$ 四人踢球打碎了玻璃窗。
$A$ 说：“是 $C$ 或 $D$ 打碎的。”
$B$ 说：“是 $D$ 打碎的。”
$C$ 说：“我没有打碎玻璃窗。”
$D$ 说：“不是我打碎的。”
他们中只有一人说了谎话。
到底是谁打碎了玻璃窗？
你认为是(D)打碎的。请写出理由。

答案： D