《2025年暑假乐园现代教育出版社四年级数学人教版》

3. 画出下面每个图形的对称轴。

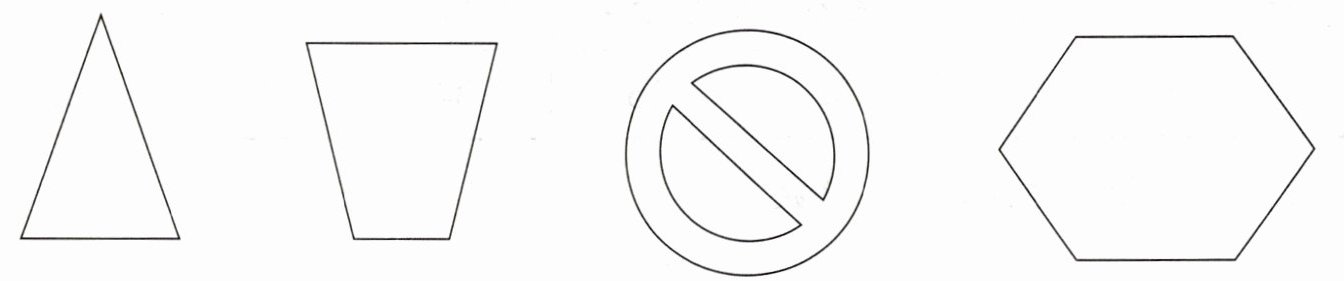
（等腰三角形有1条对称轴；等腰梯形有1条对称轴；禁止通行标志有1条对称轴；正六边形有6条对称轴）

答案： 本题可根据对称轴的定义，分别找出每个图形的对称轴并画出。
步骤一：分析第一个图形（等腰三角形）
等腰三角形沿着底边上的高对折后，直线两旁的部分能够完全重合，所以等腰三角形有$1$条对称轴，即底边上的高所在的直线。
步骤二：分析第二个图形（等腰梯形）
等腰梯形沿着上下底中点的连线对折后，直线两旁的部分能够完全重合，所以等腰梯形有$1$条对称轴，即上下底中点的连线所在的直线。
步骤三：分析第三个图形（禁止通行标志）
该图形沿着过圆心且与中间斜杠垂直的直线对折后，直线两旁的部分能够完全重合，所以它有$1$条对称轴。
步骤四：分析第四个图形（正六边形）
正六边形沿着对边中点的连线以及对角线对折后，直线两旁的部分都能够完全重合，正六边形有$6$条对称轴。
根据上述分析，用直尺和铅笔分别画出每个图形的对称轴（画图略）。
综上，答案依次为：等腰三角形$\boldsymbol{1}$条对称轴；等腰梯形$\boldsymbol{1}$条对称轴；禁止通行标志$\boldsymbol{1}$条对称轴；正六边形$\boldsymbol{6}$条对称轴 。

4. 按要求画一画。
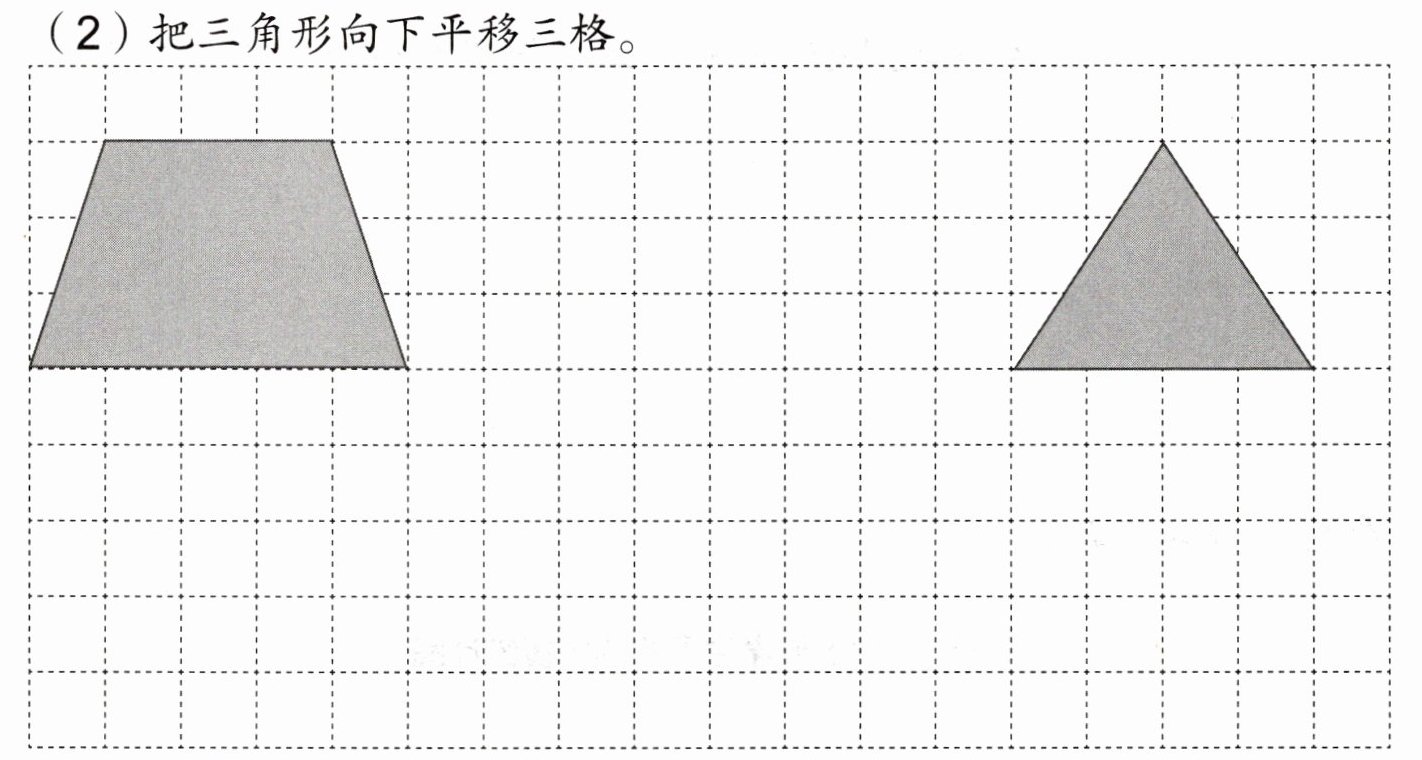
(1) 将梯形先向下平移两格，再向右平移三格。本题可根据平移的性质，通过确定梯形四个顶点（设为A、B、C、D）等关键点，先将各顶点向下平移两格得到A₁、B₁、C₁、D₁，再向右平移三格得到A₂、B₂、C₂、D₂，最后依次连接A₂、B₂、C₂、D₂即可。
(2) 把三角形向下平移三格。本题可根据平移的性质，通过确定三角形三个顶点（设为E、F、G）等关键点，将各顶点向下平移三格得到E₁、F₁、G₁，最后依次连接E₁、F₁、G₁即可。

答案： 本题可根据平移的性质，通过确定图形关键点平移后的位置，再连接各点得到平移后的图形。
$(1)$ 将梯形先向下平移两格，再向右平移三格
步骤一：确定梯形的关键点
梯形的四个顶点为关键点，设这四个顶点分别为$A$、$B$、$C$、$D$。
步骤二：对关键点进行平移
向下平移两格：根据平移的性质，向下平移时，纵坐标减少相应的格数，横坐标不变。则$A$、$B$、$C$、$D$四个点向下平移两格后得到$A_1$、$B_1$、$C_1$、$D_1$。
再向右平移三格：向右平移时，横坐标增加相应的格数，纵坐标不变。$A_1$、$B_1$、$C_1$、$D_1$再向右平移三格后得到$A_2$、$B_2$、$C_2$、$D_2$。
步骤三：连接平移后的关键点
依次连接$A_2$、$B_2$、$C_2$、$D_2$，得到先向下平移两格，再向右平移三格后的梯形。
$(2)$ 把三角形向下平移三格
步骤一：确定三角形的关键点
三角形的三个顶点为关键点，设这三个顶点分别为$E$、$F$、$G$。
步骤二：对关键点进行平移
根据平移的性质，向下平移时，纵坐标减少相应的格数，横坐标不变。将$E$、$F$、$G$三个点向下平移三格后得到$E_1$、$F_1$、$G_1$。
步骤三：连接平移后的关键点
依次连接$E_1$、$F_1$、$G_1$，得到向下平移三格后的三角形。
由于无法直接为您绘制图形，您可以按照上述步骤，在给定的方格图中完成图形的平移绘制。
综上，按照上述方法即可完成$(1)$**梯形先向下平移两格，再向右平移三格**和$(2)$**三角形向下平移三格**的图形绘制。

1. 在一片长30米、宽14米的长方形草坪上有两条相交的小路，那么草坪的面积是377平方米？

答案： （30 - 1）×（14 - 1）=377（平方米）