《2025年快乐暑假江苏凤凰教育出版社二年级数学》

1. 在计数器上一边拨珠一边数。
(1) 一十一十地数，从八百八十数到一千。
(2) 一个一个地数，从六百八十五数到七百零六。

答案： 【解析】：1. 一十一十地数，就是每次在原数的基础上加 10。从八百八十开始，依次加 10 得到后面的数，八百八十加 10 是八百九十，八百九十加 10 是九百，九百加 10 是九百一十，九百一十加 10 是九百二十，九百二十加 10 是九百三十，九百三十加 10 是九百四十，九百四十加 10 是九百五十，九百五十加 10 是九百六十，九百六十加 10 是九百七十，九百七十加 10 是九百八十，九百八十加 10 是九百九十，九百九十加 10 是一千。2. 一个一个地数，就是每次在原数的基础上加 1。从六百八十五开始，依次加 1 得到后面的数，六百八十五加 1 是六百八十六，六百八十六加 1 是六百八十七，以此类推，直到七百零六。
【答案】：1. 八百八十、八百九十、九百、九百一十、九百二十、九百三十、九百四十、九百五十、九百六十、九百七十、九百八十、九百九十、一千 2. 六百八十五、六百八十六、六百八十七、六百八十八、六百八十九、六百九十、六百九十一、六百九十二、六百九十三、六百九十四、六百九十五、六百九十六、六百九十七、六百九十八、六百九十九、七百、七百零一、七百零二、七百零三、七百零四、七百零五、七百零六

2. 读一读，画一画。

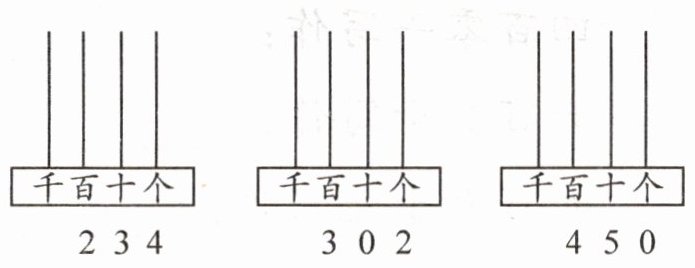
234读作二百三十四，画计数器：千位0个珠子，百位2个珠子，十位3个珠子，个位4个珠子；302读作三百零二，画计数器：千位0个珠子，百位3个珠子，十位0个珠子，个位2个珠子；450读作四百五十，画计数器：千位0个珠子，百位4个珠子，十位5个珠子，个位0个珠子。

答案： 【解析】：根据计数器读数规则，从高位读起，百位上是几就读几百，十位上是几就读几十，个位上是几就读几，中间的$0$读零，末尾的$0$不读。画计数器时，对应数位上是几就画几个珠子。$234$读作二百三十四，画计数器时千位不画珠子，百位画$2$个珠子，十位画$3$个珠子，个位画$4$个珠子；$302$读作三百零二，画计数器时千位不画珠子，百位画$3$个珠子，十位不画珠子，个位画$2$个珠子；$450$读作四百五十，画计数器时千位不画珠子，百位画$4$个珠子，十位画$5$个珠子，个位不画珠子。
【答案】：$234$读作二百三十四，画计数器：千位$0$个珠子，百位$2$个珠子，十位$3$个珠子，个位$4$个珠子；$302$读作三百零二，画计数器：千位$0$个珠子，百位$3$个珠子，十位$0$个珠子，个位$2$个珠子；$450$读作四百五十，画计数器：千位$0$个珠子，百位$4$个珠子，十位$5$个珠子，个位$0$个珠子。

五、小小数学家。
用$\boxed{4}$ $\boxed{3}$ $\boxed{8}$三张数字卡片，可以组成多少个不同的三位数？(分别写出来)

答案： 【解析】：本题可根据百位上数字的不同来进行分类讨论。当百位上是$4$时，组成的数有$438$、$483$；当百位上是$3$时，组成的数有$348$、$384$；当百位上是$8$时，组成的数有$834$、$843$。所以一共可以组成$6$个不同的三位数。
【答案】：可以组成$6$个不同的三位数，分别是$438$、$483$、$348$、$384$、$834$、$843$。