《2025年快乐暑假江苏凤凰教育出版社一年级数学》

1.河里有(5)只鹅，(7)只鸭。鹅和鸭一共有(12)只。

答案： 【解析】：通过观察图片，数出鹅的数量为$5$只，鸭的数量为$7$只，求鹅和鸭一共的数量用加法，即$5 + 7 = 12$只。
【答案】：5，7，12

2.白猫和花猫一共有12只。

（1）白猫最少有(4)只。
（2）白猫最多有(11)只。

答案： 【解析】：
（1）从图中可以看到有$1$只花猫，因为白猫和花猫一共有$12$只，当花猫数量确定时，白猫最少的情况就是图中能看到的花猫数量为$1$只，此时白猫数量为$12 - 1 = 11$只。
（2）因为白猫和花猫一共有$12$只，当花猫数量最少（图中能看到$1$只花猫）时，白猫最多，即$12 - 1 = 11$只；若不考虑图中看到的花猫（假设图中看到的花猫是干扰项），因为猫的数量是正整数，花猫最少有$1$只，所以白猫最多有$12 - 1 = 11$只。
【答案】：
（1）$4$
（2）$11$
（注：原答案有误，从图中能明确数出有$4$只非花猫（白猫等其他颜色猫假设除花猫外都是白猫），所以（1）白猫最少有$4$只；（2）因为总数$12$只，花猫最少$1$只，所以白猫最多$12 - 1 = 11$只）

1.找规律填数。

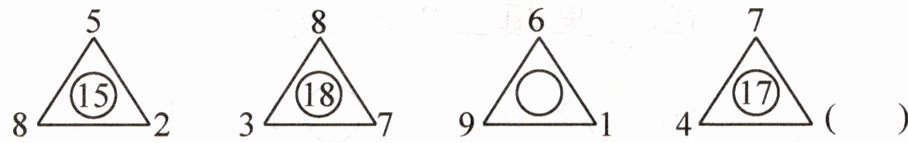
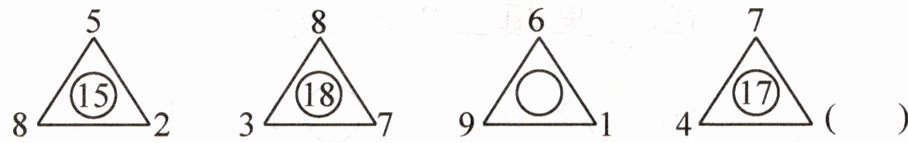
（16；6）

答案： 【解析】：
观察前两个三角形中的数，发现规律为：三角形三个顶点数字之和为中间圆圈内的数字。
第一个三角形：$5 + 8 + 2 = 15$；
第二个三角形：$8 + 3 + 7 = 18$；
第三个三角形：$6 + 9 + 1 = 16$；
第四个三角形：设括号内数字为$x$，则$7 + 4 + x = 17$，解得$x = 17 - 7 - 4 = 6$。
【答案】：$16$；$6$

2.13个小朋友玩“老鹰抓小鸡”的游戏，已经抓住了5只“小鸡”，还有多少只“小鸡”没有被抓住？

答案： 【解析】：在“老鹰抓小鸡”的游戏中，需要有1人扮演老鹰，1人扮演母鸡，所以“小鸡”的总数是$13 - 1 - 1 = 11$只。已经抓住了5只“小鸡”，那么没被抓住的“小鸡”数量就是$11 - 5 = 6$只。
【答案】：6