第63页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
(4)1千克黄豆能做4千克豆腐。豆腐店有12袋黄豆,每袋50千克,这些黄豆能做多少千克豆腐?
答案:
【解析】:先计算出黄豆的总重量,用每袋黄豆的重量乘以黄豆的袋数,即$12\times50 = 600$千克。已知1千克黄豆能做4千克豆腐,那么600千克黄豆能做的豆腐重量为黄豆总重量乘以每千克黄豆能做的豆腐重量,也就是$600\times4 = 2400$千克。
【答案】:2400
【答案】:2400
(5)小明、小红、小林、小芳一起坐在椅子上拍照,如果小明坐在最左边不动,其他人可以任意换位置,最多有多少种坐法?
答案:
【解析】:因为小明坐在最左边不动,那么只需要考虑小红、小林、小芳三人的排列顺序。对于三个人进行全排列,根据排列组合的知识,第一个位置有3种选择(小红、小林、小芳三人中选一个),选了一个人后,第二个位置就剩下2种选择,第三个位置就只有1种选择。根据排列数公式$A_{n}^m=\frac{n!}{(n - m)!}$,这里$n=3$,$m = 3$,$A_{3}^3=\frac{3!}{(3-3)!}=3\times2\times1 = 6$种坐法,也可以通过列举法:当小红在小明右边第二个位置时,小林和小芳有2种坐法(小林第三、小芳第四;小芳第三、小林第四);当小林在小明右边第二个位置时,小红和小芳有2种坐法;当小芳在小明右边第二个位置时,小红和小林有2种坐法,总共$2+2+2 = 6$种坐法。
【答案】:6
【答案】:6
数学小实践
在下面的方格里画一些面积是12平方厘米的不同长方形,并算出它们的周长。你能画几个?(每个方格的边长表示1厘米。)
在下面的方格里画一些面积是12平方厘米的不同长方形,并算出它们的周长。你能画几个?(每个方格的边长表示1厘米。)
答案:
【答案】:能画$3$个,长$12$厘米、宽$1$厘米的长方形周长是$26$厘米;长$6$厘米、宽$2$厘米的长方形周长是$16$厘米;长$4$厘米、宽$3$厘米的长方形周长是$14$厘米。
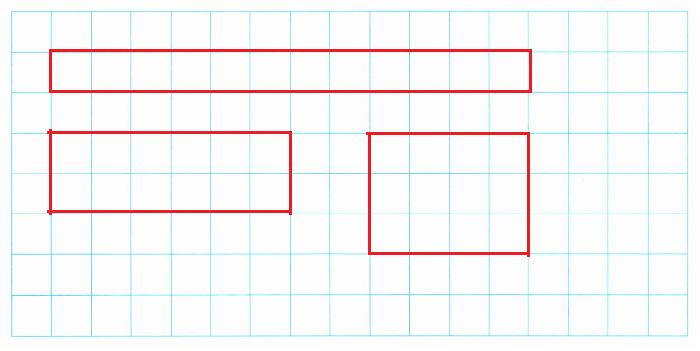
【答案】:能画$3$个,长$12$厘米、宽$1$厘米的长方形周长是$26$厘米;长$6$厘米、宽$2$厘米的长方形周长是$16$厘米;长$4$厘米、宽$3$厘米的长方形周长是$14$厘米。

查看更多完整答案,请扫码查看


