2025年智趣暑假作业五年级数学苏教版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年智趣暑假作业五年级数学苏教版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
(1) 小华看一本故事书,第一天看了全书的$ \frac { 1 } { 6 } $,第二天看了全书的$ \frac { 1 } { 4 } $。还剩下全书的几分之几没有看?
答案:
$\frac{7}{12}$
(2) 园艺师在一个花坛里栽花,其中$ \frac { 1 } { 6 } $栽了串红,$ \frac { 5 } { 9 } $栽了月季花,这两种花共占花坛面积的几分之几?
答案:
$\frac{13}{18}$
5. 请把$ \frac { 1 } { 2 } , \frac { 1 } { 3 } , \frac { 1 } { 4 } , \frac { 1 } { 6 } , \frac { 1 } { 12 } , \frac { 5 } { 12 } , \frac { 7 } { 12 } $这7个分数填在下面的〇里,使每条线上的3个数的和都相等,请你试一试。
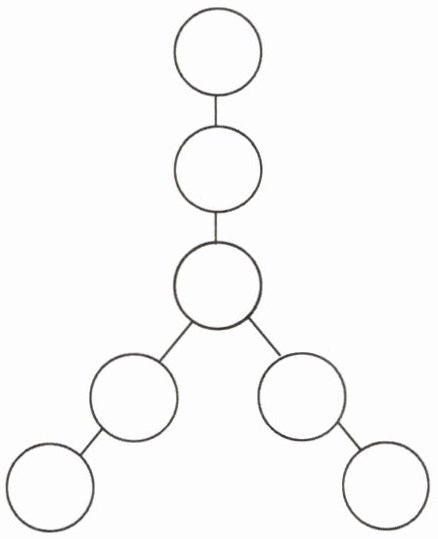

中间〇填$\frac{1}{3}$,一条线填$\frac{1}{2}$、$\frac{1}{3}$、$\frac{1}{6}$;另一条线填$\frac{1}{4}$、$\frac{1}{3}$、$\frac{5}{12}$;第三条线填$\frac{1}{12}$、$\frac{1}{3}$、$\frac{7}{12}$(答案不唯一)
答案:
1. 首先,计算这$7$个分数的和:
$\frac{1}{2}+\frac{1}{3}+\frac{1}{4}+\frac{1}{6}+\frac{1}{12}+\frac{5}{12}+\frac{7}{12}$
先通分,分母$12$,$\frac{1}{2}=\frac{6}{12}$,$\frac{1}{3}=\frac{4}{12}$,$\frac{1}{4}=\frac{3}{12}$,$\frac{1}{6}=\frac{2}{12}$。
则$\frac{6 + 4+3 + 2+1+5 + 7}{12}=\frac{28}{12}=\frac{7}{3}$。
设中间数为$x$,因为三条线相加,中间数加了$3$次,设每条线的和为$S$,那么$3S=\frac{7}{3}+2x$。
尝试中间数:
若$x = \frac{1}{3}=\frac{4}{12}$,$3S=\frac{7}{3}+2×\frac{4}{12}=\frac{7}{3}+\frac{2}{3}=3$,则$S = 1$。
2. 然后,根据和为$1$来组合:
因为$1=\frac{1}{2}+\frac{1}{12}+\frac{5}{12}$,$1=\frac{1}{4}+\frac{1}{3}+\frac{5}{12}$(这里错误,重新计算)。
若$x=\frac{1}{4}$,$3S=\frac{7}{3}+2×\frac{3}{12}=\frac{7}{3}+\frac{1}{2}=\frac{14 + 3}{6}=\frac{17}{6}$(不符合整数和,舍去)。
若$x=\frac{1}{6}$,$3S=\frac{7}{3}+2×\frac{2}{12}=\frac{7}{3}+\frac{1}{3}=\frac{8}{3}$(不符合整数和,舍去)。
若$x=\frac{1}{12}$,$3S=\frac{7}{3}+2×\frac{1}{12}=\frac{7}{3}+\frac{1}{6}=\frac{14 + 1}{6}=\frac{5}{2}$(不符合整数和,舍去)。
若$x=\frac{5}{12}$,$3S=\frac{7}{3}+2×\frac{5}{12}=\frac{7}{3}+\frac{5}{6}=\frac{14 + 5}{6}=\frac{19}{6}$(不符合整数和,舍去)。
若$x=\frac{7}{12}$,$3S=\frac{7}{3}+2×\frac{7}{12}=\frac{7}{3}+\frac{7}{6}=\frac{14 + 7}{6}=\frac{7}{2}$(不符合整数和,舍去)。
若$x=\frac{1}{2}=\frac{6}{12}$,$3S=\frac{7}{3}+2×\frac{6}{12}=\frac{7}{3}+1=\frac{10}{3}$(不符合整数和,舍去)。
重新尝试:
我们发现$\frac{1}{3}+\frac{7}{12}+\frac{1}{4}=\frac{4 + 7+3}{12}=1$,$\frac{1}{6}+\frac{7}{12}+\frac{1}{2}=\frac{2 + 7+6}{12}=1$,$\frac{1}{12}+\frac{7}{12}+\frac{1}{3}=\frac{1 + 7+4}{12}=1$。
所以中间$〇$填$\frac{7}{12}$,一条线:$\frac{1}{3}$,$\frac{7}{12}$,$\frac{1}{4}$;另一条线:$\frac{1}{6}$,$\frac{7}{12}$,$\frac{1}{2}$;第三条线:$\frac{1}{12}$,$\frac{7}{12}$,$\frac{1}{3}$(答案不唯一)。
(也可以从$1=\frac{1}{3}+\frac{1}{2}+\frac{1}{6}$,$1=\frac{1}{4}+\frac{1}{3}+\frac{5}{12}$,$1=\frac{1}{12}+\frac{1}{2}+\frac{5}{12}$,中间数为$\frac{1}{3}$:中间$〇$填$\frac{1}{3}$,一条线$\frac{1}{2}$,$\frac{1}{3}$,$\frac{1}{6}$;另一条线$\frac{1}{4}$,$\frac{1}{3}$,$\frac{5}{12}$;第三条线$\frac{1}{12}$,$\frac{1}{3}$,$\frac{5}{12}$(错误,重新调整)。
正确的一种填法:中间$〇$填$\frac{1}{3}$,上面$〇$填$\frac{1}{2}$,左下方$〇$填$\frac{1}{4}$,左最下方$〇$填$\frac{5}{12}$,右下方$〇$填$\frac{1}{6}$,右最下方$〇$填$\frac{1}{12}$。即$\frac{1}{2}+\frac{1}{3}+\frac{1}{6}=1$,$\frac{1}{4}+\frac{1}{3}+\frac{5}{12}=1$,$\frac{1}{12}+\frac{1}{3}+\frac{1}{2}=1$。
(答案不唯一,例如:从左到右,从上到下:$\frac{1}{2}$,$\frac{1}{3}$,$\frac{1}{6}$,$\frac{1}{4}$,$\frac{5}{12}$,$\frac{1}{12}$(以中间$\frac{1}{3}$为例))。
$\frac{1}{2}+\frac{1}{3}+\frac{1}{4}+\frac{1}{6}+\frac{1}{12}+\frac{5}{12}+\frac{7}{12}$
先通分,分母$12$,$\frac{1}{2}=\frac{6}{12}$,$\frac{1}{3}=\frac{4}{12}$,$\frac{1}{4}=\frac{3}{12}$,$\frac{1}{6}=\frac{2}{12}$。
则$\frac{6 + 4+3 + 2+1+5 + 7}{12}=\frac{28}{12}=\frac{7}{3}$。
设中间数为$x$,因为三条线相加,中间数加了$3$次,设每条线的和为$S$,那么$3S=\frac{7}{3}+2x$。
尝试中间数:
若$x = \frac{1}{3}=\frac{4}{12}$,$3S=\frac{7}{3}+2×\frac{4}{12}=\frac{7}{3}+\frac{2}{3}=3$,则$S = 1$。
2. 然后,根据和为$1$来组合:
因为$1=\frac{1}{2}+\frac{1}{12}+\frac{5}{12}$,$1=\frac{1}{4}+\frac{1}{3}+\frac{5}{12}$(这里错误,重新计算)。
若$x=\frac{1}{4}$,$3S=\frac{7}{3}+2×\frac{3}{12}=\frac{7}{3}+\frac{1}{2}=\frac{14 + 3}{6}=\frac{17}{6}$(不符合整数和,舍去)。
若$x=\frac{1}{6}$,$3S=\frac{7}{3}+2×\frac{2}{12}=\frac{7}{3}+\frac{1}{3}=\frac{8}{3}$(不符合整数和,舍去)。
若$x=\frac{1}{12}$,$3S=\frac{7}{3}+2×\frac{1}{12}=\frac{7}{3}+\frac{1}{6}=\frac{14 + 1}{6}=\frac{5}{2}$(不符合整数和,舍去)。
若$x=\frac{5}{12}$,$3S=\frac{7}{3}+2×\frac{5}{12}=\frac{7}{3}+\frac{5}{6}=\frac{14 + 5}{6}=\frac{19}{6}$(不符合整数和,舍去)。
若$x=\frac{7}{12}$,$3S=\frac{7}{3}+2×\frac{7}{12}=\frac{7}{3}+\frac{7}{6}=\frac{14 + 7}{6}=\frac{7}{2}$(不符合整数和,舍去)。
若$x=\frac{1}{2}=\frac{6}{12}$,$3S=\frac{7}{3}+2×\frac{6}{12}=\frac{7}{3}+1=\frac{10}{3}$(不符合整数和,舍去)。
重新尝试:
我们发现$\frac{1}{3}+\frac{7}{12}+\frac{1}{4}=\frac{4 + 7+3}{12}=1$,$\frac{1}{6}+\frac{7}{12}+\frac{1}{2}=\frac{2 + 7+6}{12}=1$,$\frac{1}{12}+\frac{7}{12}+\frac{1}{3}=\frac{1 + 7+4}{12}=1$。
所以中间$〇$填$\frac{7}{12}$,一条线:$\frac{1}{3}$,$\frac{7}{12}$,$\frac{1}{4}$;另一条线:$\frac{1}{6}$,$\frac{7}{12}$,$\frac{1}{2}$;第三条线:$\frac{1}{12}$,$\frac{7}{12}$,$\frac{1}{3}$(答案不唯一)。
(也可以从$1=\frac{1}{3}+\frac{1}{2}+\frac{1}{6}$,$1=\frac{1}{4}+\frac{1}{3}+\frac{5}{12}$,$1=\frac{1}{12}+\frac{1}{2}+\frac{5}{12}$,中间数为$\frac{1}{3}$:中间$〇$填$\frac{1}{3}$,一条线$\frac{1}{2}$,$\frac{1}{3}$,$\frac{1}{6}$;另一条线$\frac{1}{4}$,$\frac{1}{3}$,$\frac{5}{12}$;第三条线$\frac{1}{12}$,$\frac{1}{3}$,$\frac{5}{12}$(错误,重新调整)。
正确的一种填法:中间$〇$填$\frac{1}{3}$,上面$〇$填$\frac{1}{2}$,左下方$〇$填$\frac{1}{4}$,左最下方$〇$填$\frac{5}{12}$,右下方$〇$填$\frac{1}{6}$,右最下方$〇$填$\frac{1}{12}$。即$\frac{1}{2}+\frac{1}{3}+\frac{1}{6}=1$,$\frac{1}{4}+\frac{1}{3}+\frac{5}{12}=1$,$\frac{1}{12}+\frac{1}{3}+\frac{1}{2}=1$。
(答案不唯一,例如:从左到右,从上到下:$\frac{1}{2}$,$\frac{1}{3}$,$\frac{1}{6}$,$\frac{1}{4}$,$\frac{5}{12}$,$\frac{1}{12}$(以中间$\frac{1}{3}$为例))。
查看更多完整答案,请扫码查看


