第51页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
2. 用竖式计算。
$5.82+2.58= $ $1.66-1.04= $ $16.7-1.58= $
$5.82+2.58= $ $1.66-1.04= $ $16.7-1.58= $
答案:
8.4
0.62
15.12
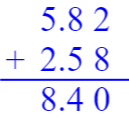
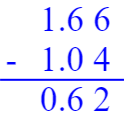
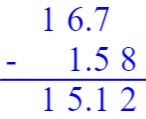
8.4
0.62
15.12
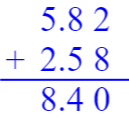
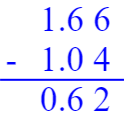
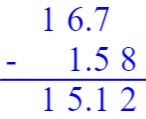
3. 计算下面每个图形的面积。


答案:
25×16=400(平方厘米)
40×10÷2=200(平方分米)
(40+50)×30÷2=1350(平方米)
40×10÷2=200(平方分米)
(40+50)×30÷2=1350(平方米)
1. 在30、30.0、0.30、0.030中,去掉末尾的“0”后大小改变的是( )。
① 30 ② 30.0 ③ 0.30 ④ 0.030
① 30 ② 30.0 ③ 0.30 ④ 0.030
答案:
①
2. 10里面有( )个0.1。
① 10 ② 100 ③ 1000 ④ 1
① 10 ② 100 ③ 1000 ④ 1
答案:
②
3. 一个两位小数保留一位小数后是5.0,这个小数最大是( )。
① 4.99 ② 5.04 ③ 5.99 ④ 5.09
① 4.99 ② 5.04 ③ 5.99 ④ 5.09
答案:
②
4. 两个三角形等底等高,说明这两个三角形( )
① 形状相同 ② 面积相等
③ 能拼成一个平行四边形 ④ 完全相同
① 形状相同 ② 面积相等
③ 能拼成一个平行四边形 ④ 完全相同
答案:
②
5. 一个三角形,底扩大到原来的6倍,高缩小一半,那么这个三角形的面积( )。
① 扩大到原来的6倍 ② 缩小一半
③ 不变 ④ 扩大到原来的3倍
① 扩大到原来的6倍 ② 缩小一半
③ 不变 ④ 扩大到原来的3倍
答案:
④
6. 下面与0最接近的数是( )。
① -2 ② -1 ③ 2 ④ 1.5
① -2 ② -1 ③ 2 ④ 1.5
答案:
②
1. (1) 右边梯形的面积是多少?
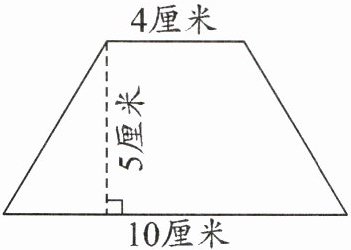
(2) 如果把这个梯形的上底增加1厘米,下底减少1厘米,得到的新梯形和原梯形的面积之间有什么关系?
(3) 如果梯形的上底增加2厘米,下底减少2厘米,得到的新梯形和原梯形的面积之间又有什么关系?
(4) 你发现了什么?尝试说明理由。

(2) 如果把这个梯形的上底增加1厘米,下底减少1厘米,得到的新梯形和原梯形的面积之间有什么关系?
(3) 如果梯形的上底增加2厘米,下底减少2厘米,得到的新梯形和原梯形的面积之间又有什么关系?
(4) 你发现了什么?尝试说明理由。
答案:
(4+10)×5÷2=35 (平方厘米)
答:梯形的面积是35平方厘米。
4+1=5 (厘米)
10-1=9 (厘米)
(5+9)×5÷2=35 (平方厘米)
答:得到的新梯形和原梯形的面积相等。
4+2=6(厘米)
10-2=8 (厘米)
(6+8) ×5÷2=35 (平方厘米)
答:得到的新梯形和原梯形的面积相等。
答:发现梯形的上底增加的长度与下底减少的长度相同,高不变时,梯形的面积不变。
理由:梯形上、下底的和不变,且梯形的高不变,那么梯形的面积就不变。
答:梯形的面积是35平方厘米。
4+1=5 (厘米)
10-1=9 (厘米)
(5+9)×5÷2=35 (平方厘米)
答:得到的新梯形和原梯形的面积相等。
4+2=6(厘米)
10-2=8 (厘米)
(6+8) ×5÷2=35 (平方厘米)
答:得到的新梯形和原梯形的面积相等。
答:发现梯形的上底增加的长度与下底减少的长度相同,高不变时,梯形的面积不变。
理由:梯形上、下底的和不变,且梯形的高不变,那么梯形的面积就不变。
查看更多完整答案,请扫码查看


