
科目: 来源: 题型:
【题目】我国魏晋时期著名的数学家刘徽在《九章算术》中提出了“割圆术——割之弥细,所失弥少,隔之又割,以至不可割,则与圆周合体,而无所失也.”也就是利用圆的内接多边形逐步逼近圆的方法来近似计算圆的面积和周长.如图1,若用圆的内接正六边形的面积![]() 来近似估计半径为1的⊙O的面积,再用如图2的圆的内接正十二边形的面积
来近似估计半径为1的⊙O的面积,再用如图2的圆的内接正十二边形的面积![]() 来近似估计半径为1的⊙O的面积,则
来近似估计半径为1的⊙O的面积,则![]() ____.(结果保留根号)
____.(结果保留根号)

查看答案和解析>>
科目: 来源: 题型:
【题目】在平面直角坐标系![]() 中,已知抛物线
中,已知抛物线![]() 与
与![]() 轴交于
轴交于![]() ,
,![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() .
.
(1)求抛物线的函数表达式
(2)如图1,点![]() 为第四象限抛物线上一点,连接
为第四象限抛物线上一点,连接![]() ,
,![]() 交于点
交于点![]() ,连接
,连接![]() ,记
,记![]() 的面积为
的面积为![]() ,
,![]() 的面积为
的面积为![]() ,求
,求![]() 的最大值;
的最大值;
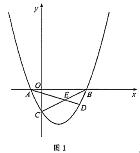
(3)如图2,连接![]() ,
,![]() ,过点
,过点![]() 作直线
作直线![]() ,点
,点![]() ,
,![]() 分别为直线和抛物线上的点.试探究:在第一象限是否存在这样的点
分别为直线和抛物线上的点.试探究:在第一象限是否存在这样的点![]() ,
,![]() ,使
,使![]() .若存在,请求出所有符合条件的点
.若存在,请求出所有符合条件的点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.

查看答案和解析>>
科目: 来源: 题型:
【题目】在矩形![]() 的
的![]() 边上取一点
边上取一点![]() ,将
,将![]() 沿
沿![]() 翻折,使点
翻折,使点![]() 恰好落在
恰好落在![]() 边上点
边上点![]() 处.
处.
(1)如图1,若![]() ,求
,求![]() 的度数;
的度数;
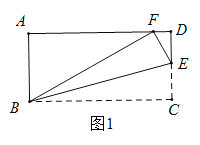
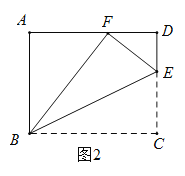
(2)如图2,当![]() ,且
,且![]() 时,求
时,求![]() 的长;
的长;
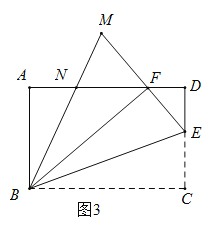
(3)如图3,延长![]() ,与
,与![]() 的角平分线交于点
的角平分线交于点![]() ,
,![]() 交
交![]() 于点
于点![]() ,当
,当![]() 时,求
时,求![]() 出的值.
出的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】在“新冠”疫情期间,全国人民“众志成城,同心抗疫”,某商家决定将一个月获得的利润全部捐赠给社区用于抗疫.已知商家购进一批产品,成本为10元/件,拟采取线上和线下两种方式进行销售.调查发现,线下的月销量![]() (单位:件)与线下售价
(单位:件)与线下售价![]() (单位:元/件,
(单位:元/件,![]() )满足一次函数的关系,部分数据如下表:
)满足一次函数的关系,部分数据如下表:

(1)求![]() 与
与![]() 的函数关系式;
的函数关系式;
(2)若线上售价始终比线下每件便宜2元,且线上的月销量固定为400件.试问:当![]() 为多少时,线上和线下月利润总和达到最大?并求出此时的最大利润.
为多少时,线上和线下月利润总和达到最大?并求出此时的最大利润.
查看答案和解析>>
科目: 来源: 题型:
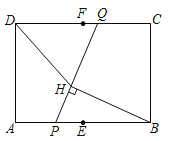
【题目】如图,在矩形![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() 分别为
分别为![]() ,
,![]() 边的中点.动点
边的中点.动点![]() 从点
从点![]() 出发沿
出发沿![]() 向点
向点![]() 运动,同时,动点
运动,同时,动点![]() 从点
从点![]() 出发沿
出发沿![]() 向点
向点![]() 运动,连接
运动,连接![]() ,过点
,过点![]() 作
作![]() 于点
于点![]() ,连接
,连接![]() .若点
.若点![]() 的速度是点
的速度是点![]() 的速度的2倍,在点
的速度的2倍,在点![]() 从点
从点![]() 运动至点
运动至点![]() 的过程中,线段
的过程中,线段![]() 长度的最大值为_________,线段
长度的最大值为_________,线段![]() 长度的最小值为_________.
长度的最小值为_________.
查看答案和解析>>
科目: 来源: 题型:
【题目】在平面直角坐标系![]() 中,已知直线
中,已知直线![]() (
(![]() )与双曲线
)与双曲线![]() 交于
交于![]() ,
,![]() 两点(点
两点(点![]() 在第一象限),直线
在第一象限),直线![]() (
(![]() )与双曲线
)与双曲线![]() 交于
交于![]() ,
,![]() 两点.当这两条直线互相垂直,且四边形
两点.当这两条直线互相垂直,且四边形![]() 的周长为
的周长为![]() 时,点
时,点![]() 的坐标为_________.
的坐标为_________.
查看答案和解析>>
科目: 来源: 题型:
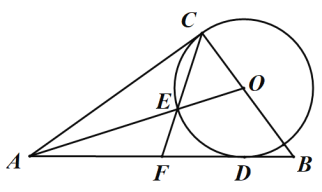
【题目】如图,在![]() 的边
的边![]() 上取一点
上取一点![]() ,以
,以![]() 为圆心,
为圆心,![]() 为半径画⊙O,⊙O与边
为半径画⊙O,⊙O与边![]() 相切于点
相切于点![]() ,
,![]() ,连接
,连接![]() 交⊙O于点
交⊙O于点![]() ,连接
,连接![]() ,并延长交线段
,并延长交线段![]() 于点
于点![]() .
.
(1)求证:![]() 是⊙O的切线;
是⊙O的切线;
(2)若![]() ,
,![]() ,求⊙O的半径;
,求⊙O的半径;
(3)若![]() 是
是![]() 的中点,试探究
的中点,试探究![]() 与
与![]() 的数量关系并说明理由.
的数量关系并说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】在平面直角坐标系![]() 中,反比例函数
中,反比例函数![]() (
(![]() )的图象经过点
)的图象经过点![]() ,过点
,过点![]() 的直线
的直线![]() 与
与![]() 轴、
轴、![]() 轴分别交于
轴分别交于![]() ,
,![]() 两点.
两点.

(1)求反比例函数的表达式;
(2)若![]() 的面积为
的面积为![]() 的面积的2倍,求此直线的函数表达式.
的面积的2倍,求此直线的函数表达式.
查看答案和解析>>
科目: 来源: 题型:
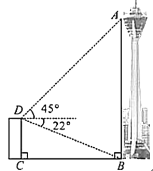
【题目】成都“339”电视塔作为成都市地标性建筑之一,现已成为外地游客到成都旅游打卡的网红地.如图,为测量电视塔观景台![]() 处的高度,某数学兴趣小组在电视塔附近一建筑物楼顶
处的高度,某数学兴趣小组在电视塔附近一建筑物楼顶![]() 处测得塔
处测得塔![]() 处的仰角为45°,塔底部
处的仰角为45°,塔底部![]() 处的俯角为22°.已知建筑物的高
处的俯角为22°.已知建筑物的高![]() 约为61米,请计算观景台的高
约为61米,请计算观景台的高![]() 的值.
的值.
(结果精确到1米;参考数据:![]() ,
,![]() ,
,![]() )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com