
科目: 来源: 题型:
【题目】如图1,抛物线y=ax2﹣6ax+6(a≠0)与x轴交于点A(8,0),与y轴交于点B,在x轴上有一动点E(m,0)(0<m<8),过点E作x轴的垂线交直线AB于点N,交抛物线于点P,过点P作PM⊥AB于点M.
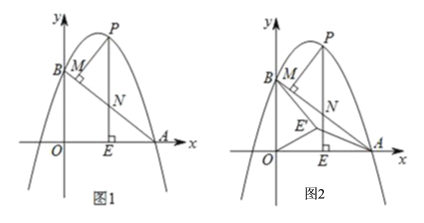
(1)求出抛物线的函数表达式;
(2)设△PMN的面积为S1,△AEN的面积为S2,若S1:S2=36:25,求m的值;
(3)如图2,在(2)条件下,将线段OE绕点O逆时针旋转得到OE′,旋转角为30°,连接E'A、E'B,在坐标平面内找一点Q,使△AOE′~△BOQ,并求出Q的坐标.
查看答案和解析>>
科目: 来源: 题型:
【题目】《郑州市城市生活垃圾分类管理办法》于2019年12月起施行,某社区要投放![]() 两种垃圾桶,负责人小李调查发现:
两种垃圾桶,负责人小李调查发现:
购买数量少于 | 购买数量不少于 | |
| 原价销售 | 以原价的 |
| 原价销售 | 以原价的 |
若购买![]() 种垃圾桶
种垃圾桶![]() 个,
个,![]() 种垃圾桶
种垃圾桶![]() 个,则共需要付款
个,则共需要付款![]() 元;若购买
元;若购买![]() 种垃圾桶
种垃圾桶![]() 个,
个,![]() 种垃圾桶
种垃圾桶![]() 个,则共需付款
个,则共需付款![]() 元.
元.
(1)求![]() 两种垃圾桶的单价各为多少元?
两种垃圾桶的单价各为多少元?
(2)若需要购买![]() 两种垃圾桶共
两种垃圾桶共![]() 个,且
个,且![]() 种垃圾桶不多于
种垃圾桶不多于![]() 种垃圾桶数量的
种垃圾桶数量的![]() ,如何购买使花费最少?最少费用为多少元?请说明理由.
,如何购买使花费最少?最少费用为多少元?请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在长方形 ABCD 中,AB=5,AD=13,点 E 为 BC 上一点,将△ABE沿 AE 折叠,使点 B 落在长方形内点 F 处,连接 DF 且 DF=12.

(1)试说明:△ADF 是直角三角形;
(2)求 BE 的长.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知抛物线![]() 的函数解析式为
的函数解析式为![]() ,若抛物线
,若抛物线![]() 经过点
经过点![]() ,对称轴为直线
,对称轴为直线![]() .
.
(1)求抛物线![]() 的解析式.
的解析式.
(2)已知实数![]() ,请证明:
,请证明:![]() ,并说明
,并说明![]() 为何值时才会有
为何值时才会有![]() .
.
(3)若抛物线![]() 先向上平移4个单位,再向左平移1个单位后得到抛物线
先向上平移4个单位,再向左平移1个单位后得到抛物线![]() ,设
,设![]() ,
,![]() 是
是![]() 上的两个不同点,且满足:
上的两个不同点,且满足:![]() ,
,![]() ,
,![]() .请你用含有
.请你用含有![]() 的表达式表示出
的表达式表示出![]() 的面积
的面积![]() ,并求出
,并求出![]() 的最小值及
的最小值及![]() 取最小值时一次函数
取最小值时一次函数![]() 的函数解析式.
的函数解析式.
(参考公式:在平面直角坐标系中,若![]() ,则
,则![]() 两点间的距离
两点间的距离![]() )
)
查看答案和解析>>
科目: 来源: 题型:
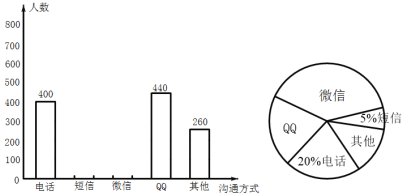
【题目】今年疫情期间,为防止疫情扩散,人们见面的机会少了,但是随着通讯技术迅猛发展,人与人之间的沟通方式更多样、便捷,为此,孙老师设计了“你最喜欢的沟通方式”调查问卷(每人必选且只选一种)进行调查.将统计结果绘制了如下两幅不完整的统计图,请结合图中所给的信息解答下列问题:
(1)这次参与调查的共有 人;在扇形统计图中,表示“微信”的扇形圆心角的度数为 ;其它沟通方式所占的百分比为 .
(2)将条形统计图补充完整;
(3)如果我国有13亿人在使用手机.
①请估计最喜欢用“微信”进行沟通的人数;
②在全国使用手机的人中随机抽取一人,用频率估计概率,求抽取的恰好使用“QQ”的概率是多少?
查看答案和解析>>
科目: 来源: 题型:
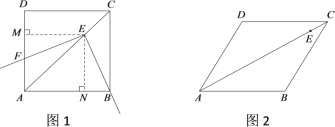
【题目】在菱形ABCD中,∠BAD=![]() ,E为对角线AC上的一点(不与A,C重合),将射线EB绕点E顺时针旋转
,E为对角线AC上的一点(不与A,C重合),将射线EB绕点E顺时针旋转![]() 角之后,所得射线与直线AD交于F点.试探究线段EB与EF的数量关系.
角之后,所得射线与直线AD交于F点.试探究线段EB与EF的数量关系.
小宇发现点E的位置,![]() 和
和![]() 的大小都不确定,于是他从特殊情况开始进行探究.
的大小都不确定,于是他从特殊情况开始进行探究.
(1)如图1,当![]() =
=![]() =90°时,菱形ABCD是正方形.小宇发现,在正方形中,AC平分∠BAD,作EM⊥AD于M,EN⊥AB于N.由角平分线的性质可知EM=EN,进而可得
=90°时,菱形ABCD是正方形.小宇发现,在正方形中,AC平分∠BAD,作EM⊥AD于M,EN⊥AB于N.由角平分线的性质可知EM=EN,进而可得![]() ,并由全等三角形的性质得到EB与EF的数量关系为 .
,并由全等三角形的性质得到EB与EF的数量关系为 .
(2)如图2,当![]() =60°,
=60°,![]() =120°时,
=120°时,
①依题意补全图形;
②请帮小宇继续探究(1)的结论是否成立.若成立,请给出证明;若不成立,请举出反例说明;
(3)小宇在利用特殊图形得到了一些结论之后,在此基础上对一般的图形进行了探究,设∠ABE=![]() ,若旋转后所得的线段EF与EB的数量关系满足(1)中的结论,请直接写出角
,若旋转后所得的线段EF与EB的数量关系满足(1)中的结论,请直接写出角![]() ,
,![]() ,
,![]() 满足的关系: .
满足的关系: .
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,一次函数y=kx+b(k≠0)的图象与反比例函数y=![]() (m≠0,x>0)的图象在第一象限内交于点A,B,且该一次函数的图象与y轴正半轴交于点C,过A,B分别作y轴的垂线,垂足分别为D,E.已知A(1,4),
(m≠0,x>0)的图象在第一象限内交于点A,B,且该一次函数的图象与y轴正半轴交于点C,过A,B分别作y轴的垂线,垂足分别为D,E.已知A(1,4),![]() =
=![]() .
.
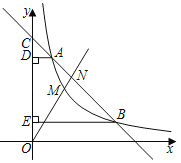
(1)求m的值和一次函数的解析式;
(2)若点M为反比例函数图象在A,B之间的动点,作射线OM交直线AB于点N,当MN长度最大时,直接写出点M的坐标.
查看答案和解析>>
科目: 来源: 题型:
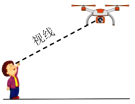
【题目】为做好疫情宣传巡查工作,各地积极借助科技手段加大防控力度.如图,亮亮在外出期间被无人机隔空喊话“戴上口罩,赶紧回家”.据测量,无人机与亮亮的水平距离是15米,当他抬头仰视无人机时,仰角恰好为![]() ,若亮亮身高1.70米,则无人机距离地面的高度约为________米.(结果精确到0.1米,参考数据:
,若亮亮身高1.70米,则无人机距离地面的高度约为________米.(结果精确到0.1米,参考数据:![]() ,
,![]() )
)
查看答案和解析>>
科目: 来源: 题型:
【题目】《九章算术》中记载:“今有上禾三秉,益实六斗,当下禾十秉.下禾五秉,益实一斗,当上禾二秉.问上、下禾实一秉各几何?”其大意是:今有上等稻子三捆,若打出来的谷子再加六斗,则相当于十捆下等稻子打出来的谷子.有下等稻子五捆,若打出来的谷子再加一斗,则相当于两捆上等稻子打岀来的谷子.问上等、下等稻子每捆能打多少斗谷子?设上等稻子每捆能打x斗谷子,下等稻子每捆能打y斗谷子,根据题意,可列方程组为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com