【题目】△ABC中,∠BAC>90°,∠ACB=∠ABC=α,点D为BC边上任意一点,点E在AD延长线上,且BC=BE.
(1)当α=30°,点D恰好为BC中点时,补全图1,求∠BEA的度数;
(2)如图2,若∠BAE=2α,此时恰好DB=DE,连接CE,求证:△ABE≌△CEB.

参考答案:
【答案】(1)30°(2)证明见解析
【解析】
(1)只要证明AE⊥BC,△BCE是等边三角形即可解决问题;
(2)如图2中,延长CA到F,使得BF=BC,则BF=BE=BC,连接BF,作BM⊥AF于M,BN⊥AE于N,只要证明Rt△BMF≌Rt△BNE,推出∠BEA=∠F,由BF=BC,推出∠F=∠C=α,推出∠BEA=α即可.
(1)补全图1,如图所示.
∵AB=AC,BD=DC,
∴AE⊥BC,
∴EB=EC,∠ADB=90°,
∵∠ABC=30°,
∴∠BAE=60°
∵BC=BE,
∴△BCE是等边三角形,∠DEB=∠DEC,
∴∠BEA=30°;
(2)延长CA到F,使得BF=BC,则BF=BE=BC,连接BF,作BM⊥AF于M,BN⊥AE于N,
∵∠ACB=∠ABC=α,
∴∠FAB=∠ABC+∠ACB=2α,
∵∠BAE=2α,
∴∠MAB=∠NAB,
∴BM=BN,
在Rt△BMF与Rt△BNE中,
![]() ,
,
∴Rt△BMF≌Rt△BNE(HL),
∴∠F=∠AEB,
∵BF=BC,
∴∠F=∠ACB=α,
∴∠AEB=α,
∴∠ACB=∠AEB,
∴A,B,E,C四点共圆,
∴∠BAE=∠ECB,
在△ABE与△CEB中,
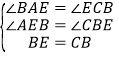 ,
,
∴ABE≌△CEB(AAS).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,方格图中每个小正方形的边长为1,点A、B、C都是格点.
(1)画出△ABC关于直线MN对称的△A1B1C1;
(2)直接写出AA1的长度;
(3)如图2,A、C是直线MN同侧固定的点,D是直线MN上的一个动点,在直线MN上画出点D,使AD+DC最小.(保留作图痕迹)

-
科目: 来源: 题型:
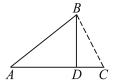
查看答案和解析>>【题目】如图所示,A,B,C,D是四个小城镇,除BC外,它们之间都有笔直的公路连接,公共汽车行驶于城镇之间,其票价与路程成正比.已知各城镇间的公共汽车票价如下: A——B:10元;A——C:12.5元;A——D:8元; B——D:6元;C——D:4.5元.为了方便B,C之间的交通,在B,C之间建成一条笔直的公路,请按上述标准计算出B,C之间公共汽车的票价为多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,某教学楼AB的后面有一建筑物CD,当光线与地面的夹角是22°时,教学楼在建筑物的墙上留下高2m的影子CE;而当光线与地面夹角是45°时,教学楼顶部A在地面上的影子F与墙角C的距离为18m(B、F、C在同一直线上).求教学楼AB的高;(结果保留整数)(参考数据:sim22°≈0.37,cos22°≈0.93,tan22°≈0.40)

-
科目: 来源: 题型:
查看答案和解析>>【题目】解不等式组
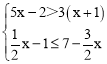 ,并将它的解集在数轴上表示出来.
,并将它的解集在数轴上表示出来. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形ABCD中,E是AD上一点,AB=8,BE=BC=10,动点P在线段BE上(与点B、E不重合),点Q在BC的延长线上,PE=CQ,PQ交EC于点F,PG∥BQ交EC于点G,设PE=x.

(1)求证:△PFG≌△QFC
(2)连结DG.当x为何值时,四边形PGDE是菱形,请说明理由; -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,等腰直角三角形ABD中,∠A=90°,AB=AD=2,作△ABD关于直线BD对称的△CBD,已知点F为线段AB上一点,且AF=m,连接CF,作∠FCE=90°,CE交AD的延长线于点E.
(1)求证:△BCF≌△DCE;
(2)若AE=n,且mn=3,求m2+n2的值.

相关试题

