【题目】如图,等腰直角三角形ABD中,∠A=90°,AB=AD=2,作△ABD关于直线BD对称的△CBD,已知点F为线段AB上一点,且AF=m,连接CF,作∠FCE=90°,CE交AD的延长线于点E.
(1)求证:△BCF≌△DCE;
(2)若AE=n,且mn=3,求m2+n2的值.

参考答案:
【答案】(1)证明见解析(2)10
【解析】
(1)首先证明四边形ABCD是正方形,再根据ASA证明△CDF≌△CBF即可;
(2)由△CDF≌△CBF,推出DE=BF=n﹣2=2﹣m,可得m+n=4,再利用完全平方公式即可解决问题;
(1)证明:∵△BCD与△BAD关于直线BD对称,
∴BA=BC,DA=DC,
∵∠A=90°,AB=AD=2,
∴AB=AD=CD=BC=2,
∴四边形ABCD是菱形,
∵∠A=90°,'
∴四边形ABCD是正方形,
∴∠DCB=∠ECF=90°,
∴∠ECD=∠FCB,
∵∠CDE=∠CBF=90°,CD=CB,
∴△CDF≌△CBF(ASA).
(2)解:∵△CDF≌△CBF,
∴DE=BF=n﹣2=2﹣m,
∴m+n=4,
∴m2+2mn+n2=16,
∵mn=3,
∴m2+n2=10.
-
科目: 来源: 题型:
查看答案和解析>>【题目】△ABC中,∠BAC>90°,∠ACB=∠ABC=α,点D为BC边上任意一点,点E在AD延长线上,且BC=BE.
(1)当α=30°,点D恰好为BC中点时,补全图1,求∠BEA的度数;
(2)如图2,若∠BAE=2α,此时恰好DB=DE,连接CE,求证:△ABE≌△CEB.

-
科目: 来源: 题型:
查看答案和解析>>【题目】解不等式组
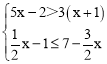 ,并将它的解集在数轴上表示出来.
,并将它的解集在数轴上表示出来. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形ABCD中,E是AD上一点,AB=8,BE=BC=10,动点P在线段BE上(与点B、E不重合),点Q在BC的延长线上,PE=CQ,PQ交EC于点F,PG∥BQ交EC于点G,设PE=x.

(1)求证:△PFG≌△QFC
(2)连结DG.当x为何值时,四边形PGDE是菱形,请说明理由; -
科目: 来源: 题型:
查看答案和解析>>【题目】小明所在的学校加强学生的体育锻炼,准备从某体育用品商店一次购买若干个足球和篮球(每个足球的价格相同,每个篮球的价格相同),若购买2个篮球和3个足球共需310元,购买5个篮球和2个足球共需500元.
(1)每个篮球和足球各需多少元?
(2)根据实际情况,需从该商店一次性购买篮球和足球功60个,要求购买篮球和足球的总费用不超过4000元,那么最多可以购买多少个篮球?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知抛物线与x轴交于A(﹣1,0),B(3,0),与y轴交于点C(0,3).

(1)求该抛物线所对应的函数关系式;
(2)设抛物线上的一个动点P的横坐标为t(0<t<0),过点P作PD⊥BC于点D.
①求线段PD的长的最大值;②当BD=2CD时,求t的值;
(3)若点Q是抛物线的对称轴上的动点,抛物线上存在点M,使得以B、C、Q、M为顶点的四边形为平行四边形,请求出所有满足条件的点M的坐标. -
科目: 来源: 题型:
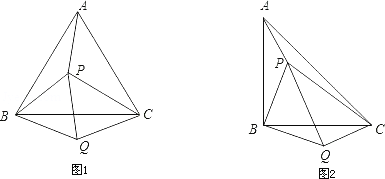
查看答案和解析>>【题目】(1)如图①所示,P是等边△ABC内的一点,连接PA、PB、PC,将△BAP绕B点顺时针旋转60°得△BCQ,连接PQ.若PA2+PB2=PC2,证明∠PQC=90°;
(2)如图②所示,P是等腰直角△ABC(∠ABC=90°)内的一点,连接PA、PB、PC,将△BAP绕B点顺时针旋转90°得△BCQ,连接PQ.当PA、PB、PC满足什么条件时,∠PQC=90°?请说明.
相关试题

