搜索
【题目】如图，在△ABC中，CE平分∠ACB，CF平分∠ACD，且EF//BC交AC于M，若CM=5，则CE2+CF2等于（ ）
A. 100 B. 75 C. 120 D. 125
参考答案：
【答案】A
【解析】
根据角平分线的定义推出△ECF为直角三角形，然后根据勾股定理即可求得CE2+CF2=EF2，进而可求出CE2+CF2的值．
∵CE平分∠ACB，CF平分∠ACD，
∴∠ACE=
∠ACB，∠ACF=∠ACD，
即∠ECF=（∠ACB+∠ACD）=90°，
∴△EFC为直角三角形，
又∵EF∥BC，CE平分∠ACB，CF平分∠ACD，
∴∠ECB=∠MEC=∠ECM，∠DCF=∠CFM=∠MCF，
∴CM=EM=MF=5，EF=10，
由勾股定理可知CE2+CF2=EF2=100．
故选：A．
-
科目： 来源： 题型：
查看答案和解析>>【题目】（背景）如图(a)，△ABC与△ADE均是顶角为40°的等腰三角形，BC，DE分别是底边，求证：BD＝CE.
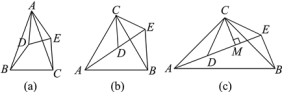
（探究）如图(b)，△ACB和△DCE均为等边三角形，点A，D，E在同一直线上，连接BE.
①∠AEB的度数为________；②线段BE与AD之间的数量关系是________．
（拓展）如图(c)，△ACB和△DCE均为等腰直角三角形，∠ACB＝∠DCE＝90°，点A，D，E在同一直线上，CM为△DCE中DE边上的高，连接BE.
①求∠AEB的度数；
②请直接写出线段CM，AE，BE之间的数量关系．
-
科目： 来源： 题型：
查看答案和解析>>【题目】在学校组织的义务植树活动中，甲、乙两组各四名同学的植树棵数如下，甲组：9，9，11，10；乙组：9，8，9，10；分别从甲、乙两组中随机选取一名同学，则这两名同学的植树总棵数为19的概率 ．
-
科目： 来源： 题型：
查看答案和解析>>【题目】操作探究：已知在纸面上有一数轴(如图所示)．
操作一：
(1)折叠纸面，使1表示的点与－1表示的点重合，则－3表示的点与________表示的点重合；
操作二：
(2)折叠纸面，使－1表示的点与3表示的点重合，回答以下问题：
①5表示的点与数________表示的点重合；
②若数轴上A、B两点之间距离为11(A在B的左侧)，且A、B两点经折叠后重合，求A、B两点表示的数是多少．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，剪两张对边平行的纸片随意交叉叠放在一起，转动其中一张，重合部分构成一个四边形，则下列结论中不一定成立的是（ ）
A. ∠DAB+∠ABC=180° B. AB=BC
C. AB=CD，AD=BC D. ∠ABC=∠ADC，∠BAD=∠BCD
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知：如图，在△ABC中，AB=AC，AD⊥BC，垂足为点D，AN是△ABC外角∠CAM的平分线，CE⊥AN，垂足为点E，
(1)求证：四边形ADCE为矩形；
(2)当△ABC满足什么条件时，四边形ADCE是一个正方形？并给出证明．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在正方形ABCD中，点E为对角线BD上一动点.若AB=
，当∠EAC=15°时，线段BE的长度为_________.
相关试题
