【题目】如图,在正方形ABCD中,点E为对角线BD上一动点.若AB=![]() ,当∠EAC=15°时,线段BE的长度为_________.
,当∠EAC=15°时,线段BE的长度为_________.

参考答案:
【答案】![]() 或
或![]()
【解析】
分两种情况:当点E在近D点时,过E作EF⊥AD于F,EM⊥AB于M,由∠CAE=15°,得出∠DAE=45°-15°=30°,设EF=x,则DF=x,AF=![]() x,根据AD-AF=DF得出
x,根据AD-AF=DF得出![]() +1-
+1-![]() x=x,从而求出EF、AM、AE的长,然后根据勾股定理求得ME的值,进而求出BE的长;当点E近B点时,同理可求BE的长.
x=x,从而求出EF、AM、AE的长,然后根据勾股定理求得ME的值,进而求出BE的长;当点E近B点时,同理可求BE的长.
解:当点E在近D点时,
过E作EF⊥AD于F,EM⊥AB于M,
∴四边形AMEF是矩形,
∵∠CAE=15°,
∴∠DAE=45°-15°=30°,
设EF=x,则DF=x,AF=![]() x,
x,
∵AD-AF=DF
∴![]() +1-
+1-![]() x=x,
x=x,
解得x=1
∴EF=AM=1
∴AF=MB=BM=![]() ,
,
∴BE=![]() =
=![]()
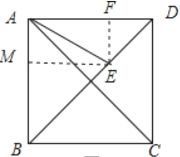
同理,当点E在近B点时,可得BE=![]() .
.
故答案为:![]() 或
或![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,CE平分∠ACB,CF平分∠ACD,且EF//BC交AC于M,若CM=5,则CE2+CF2等于( )

A. 100 B. 75 C. 120 D. 125
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,剪两张对边平行的纸片随意交叉叠放在一起,转动其中一张,重合部分构成一个四边形,则下列结论中不一定成立的是( )

A. ∠DAB+∠ABC=180° B. AB=BC
C. AB=CD,AD=BC D. ∠ABC=∠ADC,∠BAD=∠BCD
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,在△ABC中,AB=AC,AD⊥BC,垂足为点D,AN是△ABC外角∠CAM的平分线,CE⊥AN,垂足为点E,
(1)求证:四边形ADCE为矩形;
(2)当△ABC满足什么条件时,四边形ADCE是一个正方形?并给出证明.

-
科目: 来源: 题型:
查看答案和解析>>【题目】莫小贝在图1中画出△ABC,其顶点A,B,C都是格点,同时构造正方形BDEF,使它的顶点都在格点上,且它的边DE,EF分别经过点C,A,她借助此图求出了△ABC 的面积.
(1)莫小贝所画的△ABC 的三边长分别是AB=_______,BC=______,AC=______;△ABC 的面积为________.
(2)已知△ABC 中,AB=
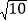 ,BC=
,BC=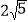 ,AC=
,AC=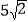 ,请你根据莫小贝的思路,在图2中画出△ABC ,并直接写出△ABC的面积_________.
,请你根据莫小贝的思路,在图2中画出△ABC ,并直接写出△ABC的面积_________.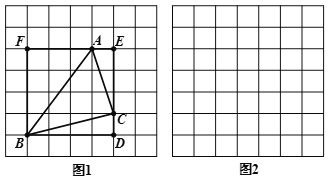
-
科目: 来源: 题型:
查看答案和解析>>【题目】在周长为26π的⊙O中,CD是⊙O的一条弦,AB是⊙O的切线,且AB∥CD,若AB和CD之间的距离为18,则弦CD的长为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC 中,∠BAC=90°,AB=AC,点D是BC上一动点,连接AD,过点A作AE⊥AD,并且始终保持AE=AD,连接CE.
(1)求证:△ABD ≌△ACE ;
(2)若AF平分∠DAE交BC于F,探究线段BD,DF,FC之间的数量关系,并证明;
(3)在(2)的条件下,若BD=3,CF=4,求AD的长.

相关试题

