【题目】(背景)如图(a),△ABC与△ADE均是顶角为40°的等腰三角形,BC,DE分别是底边,求证:BD=CE.
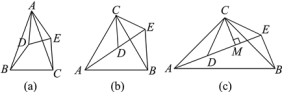
(探究)如图(b),△ACB和△DCE均为等边三角形,点A,D,E在同一直线上,连接BE.
①∠AEB的度数为________;②线段BE与AD之间的数量关系是________.
(拓展)如图(c),△ACB和△DCE均为等腰直角三角形,∠ACB=∠DCE=90°,点A,D,E在同一直线上,CM为△DCE中DE边上的高,连接BE.
①求∠AEB的度数;
②请直接写出线段CM,AE,BE之间的数量关系.
参考答案:
【答案】背景:见解析;探究:①60° ②BE=AD;拓展:(1)90°;(2)AE=BE+2CM
【解析】
背景:根据全等三角形的判定方法,判断出△BAD≌△CAE,即可判断出BD=CE;
探究:①根据△ACB和△DCE均为等边三角形,可得AC=BC,CD=CE,∠ACB=∠DCE=60°,∠CDE=∠CED=60°,据此判断出∠ACD=∠BCE;然后根据全等三角形的判定方法,判断出△ACD≌△BCE,即可判断出∠BEC=∠ADC,进而判断出∠AEB的度数为60°即可;
②,由△ACD≌△BCE,即可判断出BE=AD;
拓展:①根据△ACB和△DCE均为等腰直角三角形,可得AC=BC,CD=CE,∠ACB=∠DCE=90°,据此判断出∠ACD=∠BCE;然后根据全等三角形的判定方法,判断出△ACD≌△BCE,即可判断出BE=AD,∠BEC=∠ADC,进而判断出∠AEB的度数为90°即可;
②根据∠DCE=90°,CD=CE,CM⊥DE,可得CM=DM=EM,所以DE=DM+EM=2CM,据此判断出AE=BE+2CM即可.
背景:∵∠BAC=∠DAE=40°,
∴∠BAC-∠DAC=∠DAE-∠DAC,即∠BAD=∠CAE,
在△BAD和△CAE中,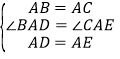 ,
,
∴△BAD≌△CAE,∴BD=CE;
探究:①∵△ACB和△DCE均为等边三角形,
∴AC=BC,CD=CE,∠ACB=∠DCE=60°,∠CDE=∠CED=60°,
∴∠ACB-∠DCB=∠DCE-∠DCB,
即∠ACD=∠BCE,
在△ACD和△BCE中,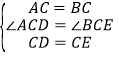 ,
,
∴△ACD≌△BCE,
∴∠ADC=∠BEC,
∵点A,D,E在同一直线上,
∴∠ADC=180-60=120°,
∴∠BEC=120°,
∴∠AEB=∠BEC-∠CED=120-60=60°,
故答案为:60°;
②∵△ACD≌△BCE,
∴BE=AD,
故答案为:BE=AD;
拓展:①∵△ACB和△DCE均为等腰直角三角形,∠ACB=∠DCE=90°,
∴AC=BC,CD=CE,∠CDE=∠CED=45°,
∠ACB-∠DCB=∠DCE-∠DCB,
即∠ACD=∠BCE,
在△ACD和△BCE中,
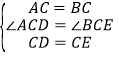 ,
,
∴△ACD≌△BCE,
∴AD=BE,∠ADC=∠BEC,
∵点A,D,E在同一直线上,
∴∠ADC=180°-∠CDE=180°-45°=135°,
∴∠BEC=135°,
∴∠AEB=∠BEC-∠CED=135°-45°=90°;
②∵∠DCE=90°,CD=CE,CM⊥DE,
∴CM=DM=EM,
∴DE=DM+EM=2CM,
又∵AD=BE,
∴AE=AD+DE=BE+2CM
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图, 在东西方向的海岸线MN上有A,B两港口,海上有一座小岛P,渔民每天都乘轮船从A,B 两港口沿AP,BP的路线去小岛捕鱼作业.已知小岛P在A港的北偏东60°方向,在B港的北偏西45°方向,小岛P距海岸线MN的距离为30海里.
(1)求AP,BP的长(参考数据:
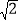 ≈1.4,
≈1.4,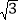 ≈1.7,
≈1.7,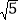 ≈2.2);
≈2.2);(2)甲、乙两船分别从A,B两港口同时出发去小岛P捕鱼作业,甲船比乙船晚到小岛24分钟.已知甲船速度是乙船速度的1.2倍,利用(1)中的结果求甲、乙两船的速度各是多少海里/时?

-
科目: 来源: 题型:
查看答案和解析>>【题目】下列各式中:
①由3x=﹣4系数化为1得x=﹣
 ;
;②由5=2﹣x移项得x=5﹣2;
③由
 去分母得2(2x﹣1)=1+3(x﹣3);
去分母得2(2x﹣1)=1+3(x﹣3);④由2(2x﹣1)﹣3(x﹣3)=1去括号得4x﹣2﹣3x﹣9=1.
其中正确的个数有( )
A. 0个 B. 1个 C. 3个 D. 4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图是某市电视台记者为了解市民获取新闻的主要图径,通过抽样调查绘制的一个条形统计图.若该市约有230万人,则可估计其中将报纸和手机上网作为获取新闻的主要途径的总人数大约为万人.
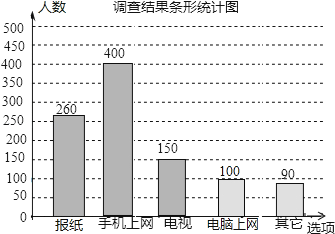
-
科目: 来源: 题型:
查看答案和解析>>【题目】在学校组织的义务植树活动中,甲、乙两组各四名同学的植树棵数如下,甲组:9,9,11,10;乙组:9,8,9,10;分别从甲、乙两组中随机选取一名同学,则这两名同学的植树总棵数为19的概率 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】操作探究:已知在纸面上有一数轴(如图所示).

操作一:
(1)折叠纸面,使1表示的点与-1表示的点重合,则-3表示的点与________表示的点重合;
操作二:
(2)折叠纸面,使-1表示的点与3表示的点重合,回答以下问题:
①5表示的点与数________表示的点重合;
②若数轴上A、B两点之间距离为11(A在B的左侧),且A、B两点经折叠后重合,求A、B两点表示的数是多少.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,CE平分∠ACB,CF平分∠ACD,且EF//BC交AC于M,若CM=5,则CE2+CF2等于( )

A. 100 B. 75 C. 120 D. 125
相关试题

