【题目】已知关于x的一元二次方程 x2-6x+m+4=0有两个实数根 x1,x2.
(1)求m的取值范围;
(2)若 x1,x2满足x2-2x1=-3 ,求m的值.
参考答案:
【答案】(1)m≤5;(2)m=5.
【解析】试题分析:
(1)由原方程有两个实数根可知:根的判别式△![]() ,由此列出关于“m”的表达式,解不等式即可求得m的取值范围;
,由此列出关于“m”的表达式,解不等式即可求得m的取值范围;
(2)由方程 x2-6x+m+4=0有两个实数根 x1,x2可得:x1+x2=6,x1·x2=m+4,结合x2-2x1=-3即可解得m的值.
试题解析:
(1)∵关于x的一元二次方程x2-6x+m+4 有实数根,
∴△ ≥0,即:△=(-6)2-4×1×(m+4)≥0 ,
∴36-4m-16≥0,解得:m≤5;
(2)∵方程 x2-6x+m+4=0有两个实数根 x1,x2,
∴ x1+x2=6,x1·x2=m+4,
又∵ x2-2x1=-3,
∴由此可解得x1=x2=3,
∴m+4=x1·x2=9,
∴m=5.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一辆汽车行驶时的平均耗油量为0.15升/千米,下面图象是油箱剩余油量
 (升)关于加满油后已行驶的路程
(升)关于加满油后已行驶的路程 (千米)的变化情况:
(千米)的变化情况:
(1)在这个变化过程中,自变量、因变量各是多少?
(2)根据图象,直接写出汽车行驶200千米时,油箱内的剩余油量,并计算加满油时油箱的油量.
(3)求
 与
与 的关系式,并计算该汽车在剩余油量5升时,已行驶的路程?
的关系式,并计算该汽车在剩余油量5升时,已行驶的路程? -
科目: 来源: 题型:
查看答案和解析>>【题目】已知射线
 平行于射线
平行于射线 ,点
,点 、
、 分别在射线
分别在射线 、
、 上.
上.
(1)如图1,若点
 在线段
在线段 上,若
上,若 ,
, 时,则
时,则 _________.
_________.(2)如图1,若点
 在线段
在线段 上运动(不包含
上运动(不包含 、
、 两点),则
两点),则 、
、 、
、 之间的等量关系是_____________________.
之间的等量关系是_____________________.(3)①如图2,若点
 在线段
在线段 的延长线上运动,则
的延长线上运动,则 、
、 、
、 之间的等量关系是________________;
之间的等量关系是________________;②如图3,若点
 在线段
在线段 的延长线上运动,则
的延长线上运动,则 、
、 、
、 之间的等量关系是________________.
之间的等量关系是________________.(4)请说明图2中所得结论的理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平行四边形ABCD中,点A1,A2,A3,A4和C1,C2,C3,C4分别是AB和CD的五等分点,点B1,B2和D1,D2分别是BC和DA的三等分点,已知四边形A4B2C4D2的面积为1cm2,则平行四边形ABCD的面积为( )cm2.

A.
 B.
B. C.
C. D.15
D.15 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点D是△ABC的边AB的延长线上一点,点F是边BC上的一个动点(不与点B重合).以BD、BF为邻边作平行四边形BDEF,又AP
 BE(点P、E在直线AB的同侧),如果
BE(点P、E在直线AB的同侧),如果 ,那么△PBC的面积与△ABC面积之比为【 】
,那么△PBC的面积与△ABC面积之比为【 】
A.
 B.
B. C.
C.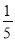 D.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,平行四边形ABCD中,AE平分∠BAD,交BC于点E,且AB=AE,延长AB与DE的延长线交于点F.下列结论中:①△ABC≌△AED;②△ABE是等边三角形;③AD=AF;④S△ABE=S△CDE;⑤S△ABE=S△CEF.其中正确的是_____.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠ACB=90°,以AC为直径作⊙O交AB于点D,E为BC的中点,连接DE并延长交AC的延长线于点F.
(1)求证:DE是⊙O的切线;
(2)若CF=2,DF=4,求⊙O直径的长.

相关试题

