【题目】如图1,已知MN∥PQ,B在MN上,C在PQ上,A在B的左侧,D在C的右侧,DE平分∠ADC,BE平分∠ABC,直线DE、BE交于点E,∠CBN=100°.
(1)若∠ADQ=130°,求∠BED的度数;
(2)将线段AD沿DC方向平移,使得点D在点C的左侧,其他条件不变,若∠ADQ=n°,求∠BED的度数(用含n的代数式表示).
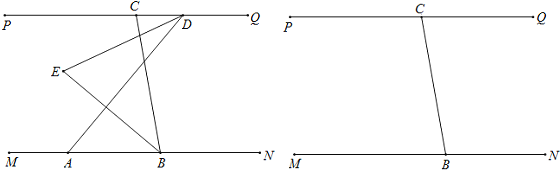
参考答案:
【答案】(1)∠BED=65°;(2)∠BED=220°﹣![]() n°.
n°.
【解析】试题分析:(1)过点E作EF∥PQ,由平行线的性质及角平分线求得∠DEF和∠FEB,即可求出∠BED的度数;
(2)过点E作EF∥PQ,由平行线的性质及角平分线求得∠DEF和∠FEB,即可求出∠BED的度数;
试题解析:
(1)如图1,过点E作EF∥PQ,
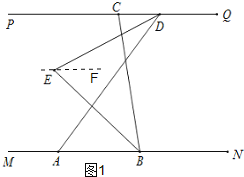
∵∠CBN=100°,∠ADQ=130°,
∴∠CBM=80°,∠ADP=50°,
∵DE平分∠ADC,BE平分∠ABC,
∴∠EBM=![]() ∠CBM=40°,
∠CBM=40°,
∠EDP=![]() ∠ADP=25°,
∠ADP=25°,
∵EF∥PQ,
∴∠DEF=∠EDP=25°,
∵EF∥PQ,MN∥PQ,
∴EF∥MN.
∴∠FEB=∠EBM=40°
∴∠BED=25°+40°=65°;
(2)如图2,过点E作EF∥PQ,
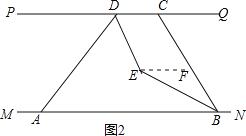
∵∠CBN=100°,
∴∠CBM=80°,
∵DE平分∠ADC,BE平分∠ABC,
∴∠EBM=![]() ∠CBM=40°,∠EDQ=
∠CBM=40°,∠EDQ=![]() ∠ADQ=
∠ADQ=![]() n°,
n°,
∵EF∥PQ,
∴∠DEF=180°﹣∠EDQ=180°﹣![]() n°,
n°,
∵EF∥PQ,MN∥PQ,
∴EF∥MN,
∴∠FEB=∠EBM=40°,
∴∠BED=180°﹣![]() n°+40°=220°﹣
n°+40°=220°﹣![]() n°.
n°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若函数y=kx|k|﹣2的图象是双曲线,且图象在第二、四象限内,那么k=
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知△ABC是等腰三角形,其边长为3和7,△DEF≌△ABC,则△DEF的周长是________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列等式一定成立的是( )
A.2a2﹣3a2=﹣a2
B.(a+2)2=a2+4
C.a6÷a3=a2
D.(a+3)(a﹣3)=a2﹣3 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形OABC中,点A、C的坐标分别为(10,0),(0,2),点D是线段BC上的动点(与端点B、C不重合),过点D作直线y=﹣
 x+m交线段OA于点E.
x+m交线段OA于点E.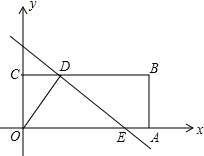
(1)矩形OABC的周长是 ;
(2)连结OD,当OD=DE时,求m的值;
(3)若矩形OABC关于直线DE的对称图形为四边形O1A1B1C1,试探究四边形O1A1B1C1与矩形OABC重叠部分的面积是否会随着E点位置的变化而变化,若不变,求出该重叠部分的面积;若改变,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某制药厂两年前生成1吨某种药品的成本是100万元,随着生产技术的进步,现在生产1吨这种药品的成本为81万元,设这种药品成本的年平均下降率为x,根据题意所列方程为( )
A.100(1+x)2=81
B.100(1﹣x)2=81
C.81(1+x)2=100
D.81(1﹣x)2=100 -
科目: 来源: 题型:
查看答案和解析>>【题目】若三角形三个内角的度数之比为2:3:5,则这个三角形一定是三角形.
相关试题

