搜索
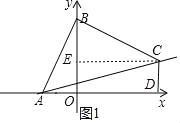
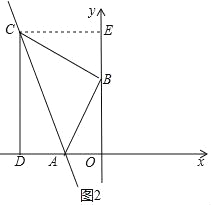
【题目】如图，在平面鱼角坐标系xOy中，A（﹣3，0），点B为y轴正半轴上一点，将线段AB绕点B旋转90°至BC处，过点C作CD垂直x轴于点D，若四边形ABCD的面积为36，则线AC的解析式为_____．
参考答案：
【答案】y＝
x+1或y＝﹣3x﹣9．
【解析】
过C作CE⊥OB于E，则四边形CEOD是矩形，得到CE＝OD，OE＝CD，根据旋转的性质得到AB＝BC，∠ABC＝90°，根据全等三角形的性质得到BO＝CE，BE＝OA，求得OA＝BE＝3，设OD＝a，得到CD＝OE＝|a﹣3|，根据面积公式列方程得到C（﹣6，9）或（6，3），设直线AB的解析式为y＝kx+b，把A点和C点的坐标代入即可得到结论．
解：过C作CE⊥OB于E，
则四边形CEOD是矩形，
∴CE＝OD，OE＝CD，
∵将线段AB绕点B旋转90°至BC处，
∴AB＝BC，
∠ABC＝90°，
∴∠ABO+∠CBO＝∠CBO+∠BCE＝90°，
∴∠ABO＝∠BCE，
∵∠AOB＝∠BEC＝90°，
∴△ABO≌△BCO（AAS），
∴BO＝CE，BE＝OA，
∵A（﹣3，0），
∴OA＝BE＝3，
设OD＝a，
∴CD＝OE＝|a﹣3|，
∵四边形ABCD的面积为36，
∴
AOOB+（CD+OB）OD＝×3×a+（a﹣3+a）×a＝36，
∴a＝±6，
∴C（﹣6，9）或（6，3），
设直线AB的解析式为y＝kx+b，
把A点和C点的坐标代入得，
或
解得：
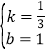或
，
∴直线AB的解析式为
或y＝﹣3x﹣9．
故答案为：或y＝﹣3x﹣9．
相关试题
科目： 来源： 题型：
【题目】如图，BD是△ABC的角平分线，点E、F分别在边BC、AB上，且DE∥AB，∠DEF=∠A．
（1）求证：BE=AF；
（2）设BD与EF交于点M，联结AE交BD于点N，求证：BNMD=BDND．
科目： 来源： 题型：
【题目】如图，在四边形ABCD中，AB∥CD，∠1=∠2，DB=DC．
（1）求证：△ABD≌△EDC；
（2）若∠A=135°，∠BDC=30°，求∠BCE的度数．
科目： 来源： 题型：
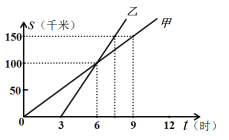
【题目】如图是甲、乙两人从同一地点出发后，路程随时间变化的图象．
（1）此变化过程中，___________ 是自变量，___________ 是因变量．
（2）甲的速度 ___________ 乙的速度.（填“大于”、“等于”、或“小于”）
（3）甲与乙 ___________ 时相遇.
（4）甲比乙先走 ___________ 小时.
（5）9时甲在乙的 ___________ （填“前面”、“后面”、“相同位置”）.
（6）路程为150km，甲行驶了___________ 小时，乙行驶了___________ 小时．
科目： 来源： 题型：
【题目】在一个不透明的袋子中装有 4 个红球和 6 个黄球，这些球除颜色外都相同，将袋子中的球充 分摇匀后，随机摸出一球.
（1）分别求摸出红球和摸出黄球的概率
（2）为了使摸出两种球的概率相同，再放进去 8 个同样的红球或黄球，那么这 8 个球中红球和 黄球的数量分别是多少？
科目： 来源： 题型：
【题目】如图，在△ABC中，已知AB＝AC，∠BAC＝90°，AH是△ABC的高，AH＝4 cm，BC＝8 cm，直线CM⊥BC，动点D从点C开始沿射线CB方向以每秒3厘米的速度运动，动点E也同时从点C开始在直线CM上以每秒1厘米的速度向远离C点的方向运动，连接AD、AE，设运动时间为t（t＞0）秒．
（1）请直接写出CD、CE的长度（用含有t的代数式表示）：CD＝ cm，CE＝ cm；
（2）当t为多少时，△ABD的面积为12 cm2？
（3）请利用备用图探究，当t为多少时，△ABD≌△ACE？并简要说明理由．
科目： 来源： 题型：
【题目】某校八（1）班同学为了解2018年姜堰某小区家庭月均用水情况，随机调查了该小区部分家庭，并将调查数据进行如下整理，请解答以下问题：
月均用水量x（t） | 频数（户） | 频率 |
0＜x≤5 | 6 | 0.12 |
5＜x≤10 | 12 | 0.24 |
10＜x≤15 | m | 0.32 |
15＜x≤20 | 10 | n |
20＜x≤25 | 4 | 0.08 |
25＜x≤30 | 2 | 0.04 |
（1）本次调查采用的调杳方式是 （填“普査”或“抽样调查”），样本容量是 ；
（2）补全频数分布直方图：
（3）若将月均用水量的频数绘成扇形统计图，则月均用水量“15＜x≤20”的圆心角度数是 ；
（4）若该小区有5000户家庭，求该小区月均用水量超过20t的家庭大约有多少户？
