【题目】如图,在四边形ABCD中,AB∥CD,∠1=∠2,DB=DC.
(1)求证:△ABD≌△EDC;
(2)若∠A=135°,∠BDC=30°,求∠BCE的度数.

参考答案:
【答案】(1)证明见解析;(2)60°.
【解析】试题分析:由全等三角形的判定方法:ASA,即可证明:△ABD≌△EDC;
(2)根据三角形内角和定理可求出∠1的度数,进而可得到∠2的度数,再根据△BDC是等腰三角形,即可求出∠BCE的度数.
试题解析:(1)证明:∵AB∥CD,∴∠ABD=∠EDC,
在△ABD和△EDC中,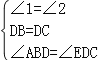 , ∴△ABD≌△EDC(ASA),
, ∴△ABD≌△EDC(ASA),
(2)解:∵∠ABD=∠EDC=30°,∠A=135°, ∴∠1=∠2=15°, ∵DB=DC,
∴∠DCB=(180°-∠DBC)=75°, ∴∠BCE=75°﹣15°=60°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,A、B、C、D在同一直线上,AB=CD,DE∥AF,若要使△ACF≌△DBE,则还需要补充一个条件:_____.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某城市对居民生活用水按以下规定收取每月的水费:家庭月用水量如果不超过8吨,按每吨2.5元收费;如果超过8吨,未超过的部分仍按每吨2.5元收取,而超过部分则按每吨4元收取.
(1)设某家庭月用水量为x吨,水费为y元,请写出y与x之间的函数解析式,并在给定的平面直角坐标系中,画出该函数的图象;
(2)如果小明家按题中规定今年3月份应缴水费34元,那么今年3月份小明家用水多少吨?

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,BD是△ABC的角平分线,点E、F分别在边BC、AB上,且DE∥AB,∠DEF=∠A.
(1)求证:BE=AF;
(2)设BD与EF交于点M,联结AE交BD于点N,求证:BNMD=BDND.

-
科目: 来源: 题型:
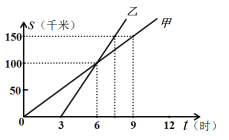
查看答案和解析>>【题目】如图是甲、乙两人从同一地点出发后,路程随时间变化的图象.
(1)此变化过程中,___________ 是自变量,___________ 是因变量.
(2)甲的速度 ___________ 乙的速度.(填“大于”、“等于”、或“小于”)
(3)甲与乙 ___________ 时相遇.
(4)甲比乙先走 ___________ 小时.
(5)9时甲在乙的 ___________ (填“前面”、“后面”、“相同位置”).
(6)路程为150km,甲行驶了___________ 小时,乙行驶了___________ 小时.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面鱼角坐标系xOy中,A(﹣3,0),点B为y轴正半轴上一点,将线段AB绕点B旋转90°至BC处,过点C作CD垂直x轴于点D,若四边形ABCD的面积为36,则线AC的解析式为_____.

-
科目: 来源: 题型:
查看答案和解析>>【题目】在一个不透明的袋子中装有 4 个红球和 6 个黄球,这些球除颜色外都相同,将袋子中的球充 分摇匀后,随机摸出一球.
(1)分别求摸出红球和摸出黄球的概率
(2)为了使摸出两种球的概率相同,再放进去 8 个同样的红球或黄球,那么这 8 个球中红球和 黄球的数量分别是多少?
相关试题

