【题目】如图,BD是△ABC的角平分线,点E、F分别在边BC、AB上,且DE∥AB,∠DEF=∠A.
(1)求证:BE=AF;
(2)设BD与EF交于点M,联结AE交BD于点N,求证:BNMD=BDND.

参考答案:
【答案】(1)见解析;(2)见解析
【解析】试题分析:(1)先证明四边形ADEF为平行四边形得到AF=DE,再证明∠DBE=∠BDE得到BE=DE,则BE=AF;
(2)如图,根据平行线分线段成比例定理,由EF∥AC得到AF:AB=DM:BD等量代换得DE:AB=DM:BD,再由DE∥AB得到DE:AB=DN:BN,则DM:BD=DN:BN,然后利用比例的性质即可得到结论.
试题解析:
证明:(1)∵DE∥AB,
∴∠A+∠ADE=180°,
∵∠DEF=∠A,
∴∠DEF+∠ADE=180°,
∴EF∥AD,
∴四边形ADEF为平行四边形,
∴AF=DE,
∵BD是△ABC的角平分线,
∴∠DBE=∠ABD,
∵DE∥AB,
∴∠ABD=∠BDE,
∴∠DBE=∠BDE,
∴BE=DE,
∴BE=AF;
(2)如图,
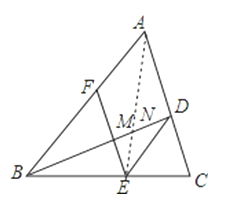
∵EF∥AC,
∴AF:AB=DM:BD,
∵AF=DE,
∴DE:AB=DM:BD,
∵DE∥AB,
∴DE:AB=DN:BN,
∴DM:BD=DN:BN,
即BN·MD=BD·ND.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,已知△ABC的三个顶点的坐标分别为A(1,0),B(2,﹣3),C(4,﹣2).
(1)画出△ABC关于x轴的对称图形△A1B1C1;
(2)画出△A1B1C1向左平移3个单位长度后得到的△A2B2C2;
(3)如果AC上有一点P(m,n)经过上述两次变换,那么对应A2C2上的点P2的坐标是 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,A、B、C、D在同一直线上,AB=CD,DE∥AF,若要使△ACF≌△DBE,则还需要补充一个条件:_____.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某城市对居民生活用水按以下规定收取每月的水费:家庭月用水量如果不超过8吨,按每吨2.5元收费;如果超过8吨,未超过的部分仍按每吨2.5元收取,而超过部分则按每吨4元收取.
(1)设某家庭月用水量为x吨,水费为y元,请写出y与x之间的函数解析式,并在给定的平面直角坐标系中,画出该函数的图象;
(2)如果小明家按题中规定今年3月份应缴水费34元,那么今年3月份小明家用水多少吨?

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四边形ABCD中,AB∥CD,∠1=∠2,DB=DC.
(1)求证:△ABD≌△EDC;
(2)若∠A=135°,∠BDC=30°,求∠BCE的度数.

-
科目: 来源: 题型:
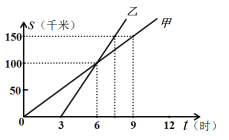
查看答案和解析>>【题目】如图是甲、乙两人从同一地点出发后,路程随时间变化的图象.
(1)此变化过程中,___________ 是自变量,___________ 是因变量.
(2)甲的速度 ___________ 乙的速度.(填“大于”、“等于”、或“小于”)
(3)甲与乙 ___________ 时相遇.
(4)甲比乙先走 ___________ 小时.
(5)9时甲在乙的 ___________ (填“前面”、“后面”、“相同位置”).
(6)路程为150km,甲行驶了___________ 小时,乙行驶了___________ 小时.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面鱼角坐标系xOy中,A(﹣3,0),点B为y轴正半轴上一点,将线段AB绕点B旋转90°至BC处,过点C作CD垂直x轴于点D,若四边形ABCD的面积为36,则线AC的解析式为_____.

相关试题

