【题目】有一个长方形绕它的一边所在的直线旋转一周,得到的几何体是圆柱.现在有一个长为6cm,宽为5cm的长方形,分别绕它的长、宽所在直线旋转一周,得到不同的圆柱,它们的体积分别是多大?
参考答案:
【答案】解:绕长所在的直线旋转一周得到圆柱体积为:π×52×6=150π(cm3);
绕宽所在的直线旋转一周得到圆柱体积为:π×62×5=180π(cm3).
答:它们的体积分别是150π(cm3)和180π(cm3).
【解析】根据圆柱体的体积=底面积×高求解,注意底面半径和高互换得圆柱体的两种情况.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知Rt△ABC≌Rt△ADE,其中∠ACB=∠AED=90°.
(1)将这两个三角形按图①方式摆放,使点E落在AB上,DE的延长线交BC于点F.求证:BF+EF=DE;
(2)改变△ADE的位置,使DE交BC的延长线于点F(如图②),则(1)中的结论还成立吗?若成立,加以证明;若不成立,写出此时BF、EF与DE之间的等量关系,并说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】“五一”期间,某市共接待海内外游客约567000人次,将567000用科学记数法表示为( )
A. 567×103 B. 56.7×104 C. 5.67×105 D. 0.567×106
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在锐角∠AOB内部画1条射线,可得3个锐角,画2条不同的射线,可得6个锐角,画3条不同的射线,可得10个锐角……照此规律,画10条不同的射线,可得锐角多少个?
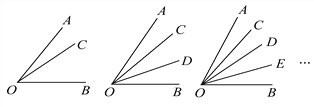
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图:在△ABC中,BE、CF分别是AC、AB两边上的高,在BE上截取BD=AC,在CF的延长线上截取CG=AB,连接AD、AG.
(1)求证:AD=AG;
(2)AD与AG的位置关系如何,请说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】下列命题正确的是( )
A.所有的直角三角形都相似B.所有的等腰三角形都相似
C.两个半径不等的圆相似D.有一个角是30°的等腰三角形都相似
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,Rt△ABC中,∠ACB=90°,∠CAB=30°.分别以AB、AC为边,向三角形外作等边△ABD和等边△ACE.
(1)如图1,连接线段BE、CD.求证:BE=CD;
(2)如图2,连接DE交AB于点F.求证:F为DE中点.
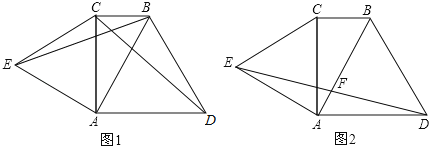
相关试题

